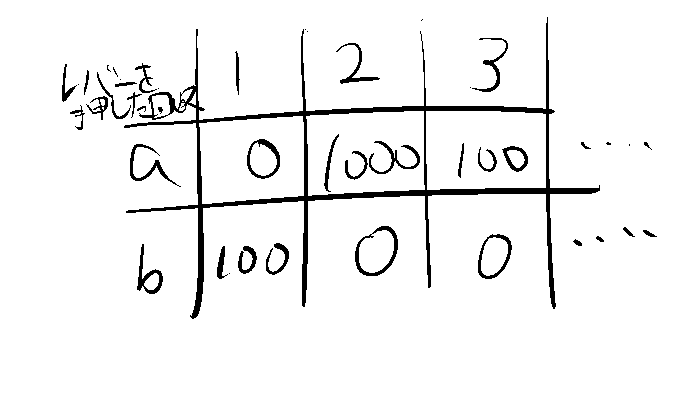更新:2024/10/09

強化学習とバンディット問題・練習問題について

$はるか$

はるか

バンディット問題は、どのスロットマシンを選べば最も報酬が得られるかを探るもの。

$ふゅか$

ふゅか

うん、まるでカジノみたいな設定だけど、実際にはさまざまな応用があるんだよ！例えば広告の最適化とか。

1. バンディット問題の問題設定
1.1. 用語の定義
1.2. 行動の定義
1.3. 報酬の定義
1.4. 報酬の推定
2. ε-greedy法について
2.1. 活用と探索
2.2. 貪欲だけ(greedy)だと
3. 練習問題

1. バンディット問題の問題設定

バンディット問題とは、画像のように複数のスロットマシンが並ぶ環境で、どのレバーを引けば最も多くの報酬を得られるかを探る問題です。プレイヤーは、各スロットマシンのレバーを引くたびに報酬を受け取りますが、どのマシンが最も高い報酬を提供するかは事前に分かりません。このような状況で、プレイヤーは最適なスロットマシンを選ぶ方法を見つける必要があります。ここで、解きたい問題はいいスロットマシンが欲しいということです。

$はるか$

はるか

複数のスロットマシンがあるとして、どれを選べばいいかって話。

$ふゅか$

ふゅか

でも、どのスロットマシンが一番儲かるかは事前にはわからないのよね。試してみないと！

1.1. 用語の定義

環境: スロットマシン。
エージェント: スロットマシンのプレイヤー。

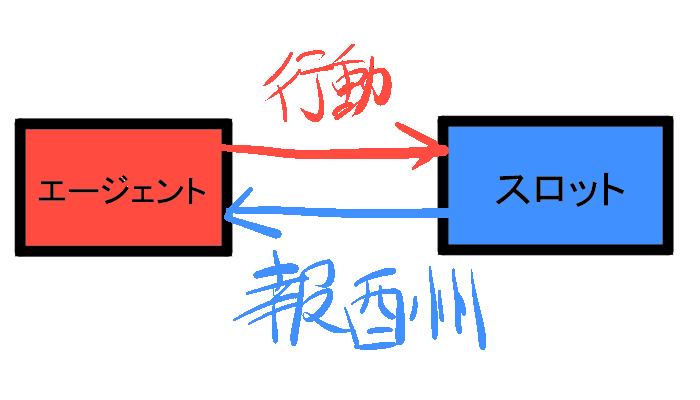
エージェントは、どのスロットマシンのレバーを引くかを決定し、その選択に応じて報酬を受け取ります。この関係を図で示すと、以下のような構図になります。

1.2. 行動の定義

エージェントの「行動」とは、どのスロットマシンのレバーを引くかを決めることです。例えば、スロットマシンが4台（a, b, c, d）ある場合、エージェントの行動 $ A $ は次のように定義されます。

$$ A = \{\text{aを選択}, \text{bを選択}, \text{cを選択}, \text{dを選択}\} $$

$はるか$

はるか

どのスロットマシンを選ぶかが「行動」。

$ふゅか$

ふゅか

選択肢が複数あるから、どれを選ぶかは重要な決断だよね。

1.3. 報酬の定義

報酬 $ R $ とは、エージェントが特定のスロットマシンを選択した際に得られる利益（例: コイン）です。報酬はスロットマシンの確率分布に依存するため、その期待値を考慮します。

エージェントが特定の行動 $ \alpha $ をとったときの報酬の条件付き期待値 $ q(\alpha) $ は、以下のように表されます。

\[ q(\alpha) = \mathbb{E}[R|A=\alpha] \]

$はるか$

はるか

報酬はスロットマシンを選んだ結果として得られるもの。

$ふゅか$

ふゅか

その報酬がどれくらいかは、実際に引いてみないと分からないのが難しいところ。

1.4. 報酬の推定

現実には、スロットマシンがどのような報酬を提供するかはエージェントには分かりません。そのため、エージェントは各スロットマシンの価値を推定する必要があります。ここで、エージェントは標本平均を用いて報酬の推定を行います。

2. ε-greedy法について

最も高い報酬を得られるスロットマシンを見つけるために、エージェントは「ε-greedy法」と呼ばれる手法を使用します。この手法では、エージェントが常に最も利益が出そうなスロットマシンを選ぶわけではなく、ランダムに他のスロットマシンも試すという戦略を組み合わせます。

2.1. 活用と探索

ε-greedy法は「活用」と「探索」を組み合わせた方法です。

活用: 既に最も利益が高いと分かっているスロットマシンを選ぶこと（greedy）。
探索: 他の可能性を試すために、意図的にgreedyでない選択をすること。

この手法では、例えば90%の確率で活用し、残りの10%の確率で探索する、といった割合で行動します。こうすることで、エージェントは既存の知識を活用しつつ、新たな可能性を探ることができるのです。

$はるか$

はるか

ε-greedy法は、常に最適を選ぶわけじゃない。

$ふゅか$

ふゅか

そう、少しだけランダムに他の選択肢も試してみるんだよ！新たな発見があるかもしれないからね。

2.2. 貪欲だけ(greedy)だと

スロットマシンの中で最も報酬が高いものを見つけることが、この問題の目的です。仮に、エージェントが常に貪欲的（greedy）に最も良さそうな選択をし続けると、予期せぬ事態に陥る可能性があります。

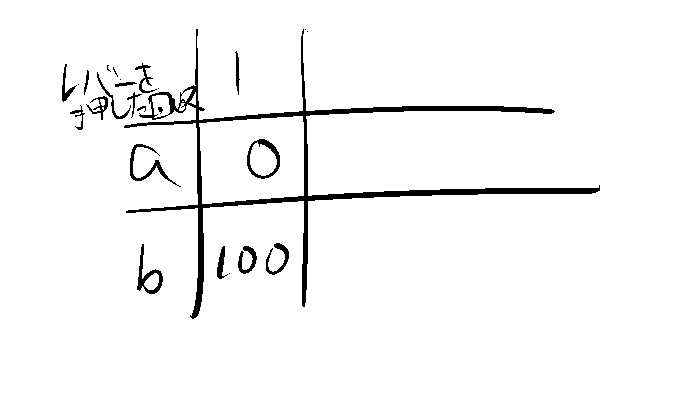
たとえば、スロットマシンが2台（a, b）あるとします。それぞれのレバーを引いたときに得られる報酬（コインの枚数）を以下の表にまとめます。

一度だけレバーを引いた場合、次のような結果になります。

この結果を見ると、bの報酬が高いため、greedyな選択をするエージェントは以後、常にbを選択することになります。

しかし、レバーを3回引いた場合の結果を見てみましょう。

この表から明らかなように、aの方がbよりも多くの報酬を得ています。このような場合、最初の貪欲な選択により、本来よりも多くの報酬を得られるスロットマシンを見逃してしまう可能性があります。

この問題が示すように、最適なスロットマシンを見つけるには、一度の選択だけではなく、複数回の試行が重要となります。

$はるか$

はるか

ちょっと例が極端な気がするけど。

3. 練習問題

あなたは、スロットマシン $a$、$b$、および $c$ の3つのスロットマシンを持っています。各スロットマシンのレバーを4回ずつ押した結果、以下の報酬が得られました。報酬の値は $R = \{0, 10, 100, 1000\}$ です。この結果をもとに、各スロットマシン $q(a)$、$q(b)$、および $q(c)$ の報酬の期待値を推定してください。

スロットマシンの報酬表