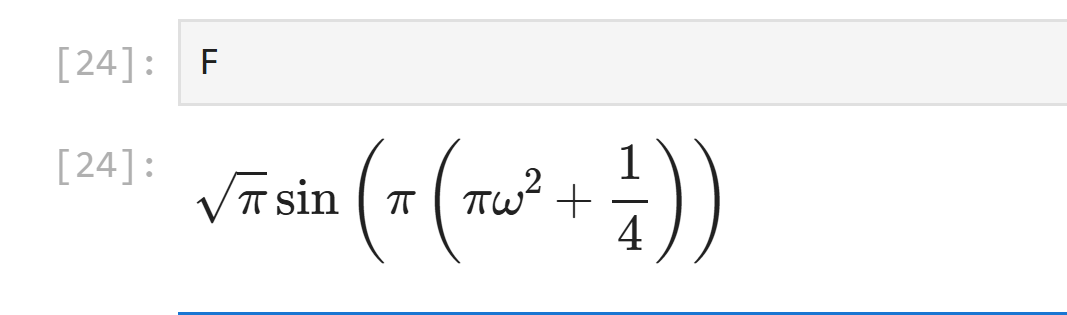マスジョイ
PR
フーリエ解析
更新:2024/11/22

【Python・SymPy】フーリエ変換とフーリエ逆変換を行う方法について

はるか
はるか
SymPy、便利。フーリエ変換も簡単。
ふゅか
ふゅか
そうそう！特に数学苦手でも、Python使えば実践的に試せるのがいいよね！
目次

1. SymPyとフーリエ変換

SymPyは、Pythonで動作する数式処理ライブラリです。本記事では、SymPyを使ってフーリエ変換を計算する方法をわかりやすく解説します。

1.1. フーリエ変換とは？

フーリエ変換は、時間領域（または空間領域）の関数を周波数領域に変換する手法です。以下が基本的なフーリエ変換の定義式です。

\[ F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i \omega t} dt \]

ここで

  • \( f(t) \)：時間領域の関数
  • \( F(\omega) \)：周波数領域の関数（フーリエ変換結果）
  • \( \omega \)：角周波数
  • \( i \)：虚数単位

また、フーリエ変換によって得られた周波数領域の関数を時間領域に戻す際には、フーリエ逆変換を使用します。

\[ f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) e^{i \omega t} d\omega \]

はるか
はるか
フーリエ変換は時間領域の関数を周波数領域に変換する手法。
ふゅか
ふゅか
つまり、信号の周波数成分を解析できるってことだね！

2. SymPyでのフーリエ変換の基本操作

はるか
はるか
SymPyではfourier_transform関数を使う。構文はsp.fourier_transform(f, t, ω)。
ふゅか
ふゅか
関数と変数を指定するだけで変換できるんだね。

SymPyでは、fourier_transform関数を使ってフーリエ変換を計算します。この関数の基本的な構文は以下の通りです。

sp.fourier_transform(f, t, ω)
  • f：変換したい関数
  • t：元の関数の変数（時間や空間変数）
  • ω：変換後の変数（周波数）

2.1. 例1：基本的なフーリエ変換

時間領域の関数 \( f(t) = e^{-t^2} \) のフーリエ変換を計算してみましょう。

import sympy as sp

# 記号変数の定義
t, ω = sp.symbols('t ω')
f = sp.exp(-t**2)

# フーリエ変換の計算
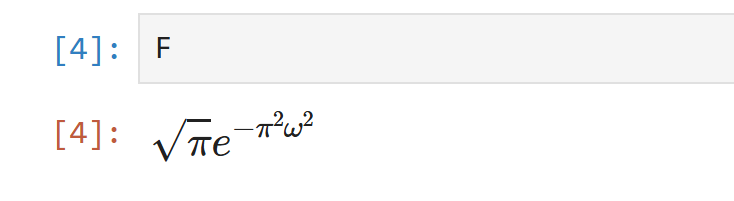
F = sp.fourier_transform(f, t, ω)
print(F)

このコードを実行すると、以下の結果が得られます。

2.2. 例2：三角関数のフーリエ変換

三角関数 \( f(t) = \cos(t^2) \) のフーリエ変換を計算します。

# Heaviside関数を用いた例
f = sp.cos(t**2)

# フーリエ変換の計算
F = sp.fourier_transform(f, t, ω)
print(F)

3. フーリエ逆変換

フーリエ変換された関数を元の時間領域に戻すには、inverse_fourier_transformを使用します。

はるか
はるか
逆変換にはinverse_fourier_transformを使用する。元の関数に戻せる。

3.1. 構文

inverse_fourier_transform(F, k, x)
  • F: フーリエ空間の関数（例: 周波数領域の関数）。
  • k: 周波数変数。
  • x: 時間変数。

3.2. 例3：逆変換の実行

上記で計算した \( F(\omega) = \sqrt{\pi} e^{-\omega^2/4} \) を逆変換して元の関数 \( f(t) \) に戻します。

# フーリエ逆変換
F=sp.sqrt(sp.pi)*sp.exp(-sp.pi**2*ω**2)
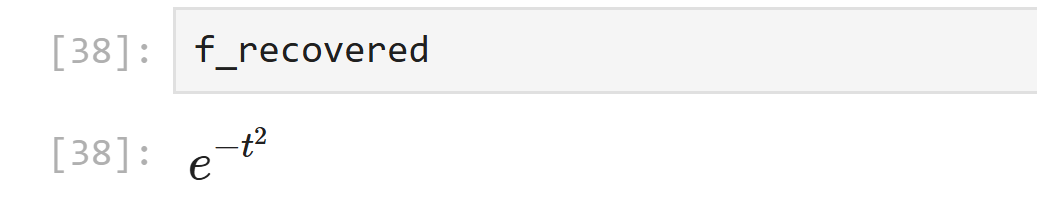
f_recovered = sp.inverse_fourier_transform(F, ω, t)

結果：

PR
ホームに戻る