マスジョイ
PR
微分積分学
更新:2024/09/17

減衰曲線e^{-x}sinxとe^{-x}cosxの極限・微分・積分・グラフについて

ふゅか
ふゅか
今回は減衰曲線についてみていこう！
はるか
はるか
減衰曲線？それってどういうもの？
ふゅか
ふゅか
例えば、時間が経つにつれて値が小さくなるものよ！
目次

1. 極限

e−xsin⁡x e^{-x}\sin x と e−xcos⁡x e^{-x}\cos x の極限は次のようになります。

lim⁡x→∞e−xsin⁡x=0,lim⁡x→∞e−xcos⁡x=0 \lim_{x \to \infty} e^{-x}\sin x = 0, \quad \lim_{x \to \infty} e^{-x}\cos x = 0

lim⁡x→−∞e−xsin⁡x=∞,lim⁡x→−∞e−xcos⁡x=∞ \lim_{x \to -\infty} e^{-x}\sin x = \infty, \quad \lim_{x \to -\infty} e^{-x}\cos x = \infty

1.1. x→∞ x \to \infty のときの極限

e−xsin⁡x e^{-x}\sin x や e−xcos⁡x e^{-x}\cos x はともに e−x e^{-x} が指数関数であり、 0 に収束するため、 sin⁡x \sin x や cos⁡x \cos x によらず 0 に収束します。 lim⁡x→∞e−xsin⁡x=0,lim⁡x→∞e−xcos⁡x=0 \lim_{x \to \infty} e^{-x}\sin x = 0, \quad \lim_{x \to \infty} e^{-x}\cos x = 0

1.2. x→−∞ x \to -\infty のときの極限

x→−∞ x \to -\infty の場合、指数関数 e−x e^{-x} が無限大に発散するため、sin⁡x \sin x や cos⁡x \cos x によらず、両方の極限は無限大になります。 lim⁡x→−∞e−xsin⁡x=∞,lim⁡x→−∞e−xcos⁡x=∞ \lim_{x \to -\infty} e^{-x}\sin x = \infty, \quad \lim_{x \to -\infty} e^{-x}\cos x = \infty

2. 微分

ふゅか
ふゅか
次は微分を見てみよう！積の微分法則を使うよ。
はるか
はるか
計算すると、両方の微分は複雑になるね。

2.1. e−xsin⁡x e^{-x}\sin x の微分

積の微分法則を使って計算します。

ddx(e−xsin⁡x)=−e−xsin⁡x+e−xcos⁡x \frac{d}{dx} \left( e^{-x}\sin x \right) = -e^{-x}\sin x + e^{-x}\cos x

2.2. e−xcos⁡x e^{-x}\cos x の微分

同様に積の微分法則を使います。

ddx(e−xcos⁡x)=−e−xsin⁡x–e−xcos⁡x \frac{d}{dx} \left( e^{-x}\cos x \right) = -e^{-x}\sin x – e^{-x}\cos x

3. 積分

e−xsin⁡x e^{-x}\sin x とe−xcos⁡x e^{-x}\cos x の積分は次のようになります。

∫e−xsin⁡x dx=−12e−x(sin⁡x+cos⁡x)+C \int e^{-x}\sin x \, dx = -\frac{1}{2}e^{-x}(\sin x + \cos x) + C

∫e−xcos⁡x dx=12e−x(sin⁡x–cos⁡x)+C \int e^{-x}\cos x \, dx = \frac{1}{2}e^{-x}(\sin x – \cos x) + C

Cは積分定数とする。

はるか
はるか
部分積分と連立方程式の二つの方法で求める。

3.1. 部分積分を利用する方法

∫e−xsin⁡x dx \int e^{-x}\sin x \, dx について部分積分を行うと次のようになります。

∫e−xsin⁡x dx=−e−xcos⁡x–∫−cos⁡x⋅(−e−x) dx \int e^{-x} \sin x \, dx = -e^{-x} \cos x – \int -\cos x \cdot (-e^{-x}) \, dx

 =−e−xcos⁡x–∫e−xcos⁡x dx  = -e^{-x} \cos x – \int e^{-x} \cos x \, dx

ここで、I=∫e−xsin⁡x dx I = \int e^{-x} \sin x \, dx 、 J=∫e−xcos⁡x dx J = \int e^{-x} \cos x \, dx とおきます。この式は次のように書き換えられます。

I=−e−xcos⁡x–J I = -e^{-x} \cos x – J

次に、J=∫e−xcos⁡x dx J = \int e^{-x} \cos x \, dx について部分積分を行います。

∫e−xcos⁡x dx=e−xsin⁡x–∫sin⁡x⋅−e−x dx \int e^{-x} \cos x \, dx = e^{-x} \sin x – \int \sin x \cdot -e^{-x} \, dx

J=e−xsin⁡x+I J = e^{-x} \sin x + I

先ほどの I I の式と合わせると、

I=−e−xcos⁡x–(e−xsin⁡x+I) I = -e^{-x} \cos x – (e^{-x} \sin x + I)

2I=−e−x(sin⁡x+cos⁡x) 2I = -e^{-x} (\sin x + \cos x)

したがって、I I は次のように求められます。

I=∫e−xsin⁡x dx=−12e−x(sin⁡x+cos⁡x)+C I = \int e^{-x} \sin x \, dx = -\frac{1}{2}e^{-x} (\sin x + \cos x) + C

同様に、先ほどの式 J=e−xsin⁡x+I J = e^{-x} \sin x + I に I=−12e−x(sin⁡x+cos⁡x) I = -\frac{1}{2}e^{-x} (\sin x + \cos x) を代入して J J を求めます。

J=e−xsin⁡x+(−12e−x(sin⁡x+cos⁡x)) J = e^{-x} \sin x + \left(-\frac{1}{2}e^{-x} (\sin x + \cos x)\right)

J=12e−x(sin⁡x–cos⁡x)+C J = \frac{1}{2}e^{-x} (\sin x – \cos x) + C

以上の計算により、次の2つの積分が求められます。

∫e−xsin⁡x dx=−12e−x(sin⁡x+cos⁡x)+C \int e^{-x} \sin x \, dx = -\frac{1}{2}e^{-x} (\sin x + \cos x) + C

∫e−xcos⁡x dx=12e−x(sin⁡x–cos⁡x)+C \int e^{-x} \cos x \, dx = \frac{1}{2}e^{-x} (\sin x – \cos x) + C

3.2. 微分した式を連立する方法

微分結果を連立させて積分を行い、積分を求めます。

ddx(e−xsin⁡x)=−e−xsin⁡x+e−xcos⁡x \frac{d}{dx} \left( e^{-x}\sin x \right) = -e^{-x}\sin x + e^{-x}\cos x

ddx(e−xcos⁡x)=−e−xsin⁡x–e−xcos⁡x \frac{d}{dx} \left( e^{-x}\cos x \right) = -e^{-x}\sin x – e^{-x}\cos x

∫e−xcos⁡x dx \displaystyle\int e^{-x} \cos x \, dx を求めます。

この2つの式を連立させて積分します。

まず、最初の微分式を整理してみます。

ddx(e−xsin⁡x)–ddx(e−xcos⁡x)=(−e−xsin⁡x+e−xcos⁡x)–(−e−xsin⁡x–e−xcos⁡x) \frac{d}{dx} \left( e^{-x}\sin x \right) – \frac{d}{dx} \left( e^{-x}\cos x \right) = \left(-e^{-x}\sin x + e^{-x}\cos x \right) – \left(-e^{-x}\sin x – e^{-x}\cos x\right)

=2e−xcos⁡x = 2e^{-x}\cos x

次に、得られた式を両辺積分します。

∫ddx(e−xsin⁡x)–ddx(e−xcos⁡x) dx=∫2e−xsin⁡x dx \int \frac{d}{dx} \left( e^{-x}\sin x \right) – \frac{d}{dx} \left( e^{-x}\cos x \right) \, dx = \int 2e^{-x}\sin x \, dx

左辺は、積分と微分が打ち消し合うため、元の関数が得られます。

e−xsin⁡x–e−xcos⁡x=∫2e−xcos⁡x dx e^{-x}\sin x – e^{-x}\cos x = \int 2e^{-x}\cos x \, dx

したがって、積分結果は次のように表されます。

∫e−xcos⁡x dx=−12(e−xsin⁡x–e−xcos⁡x)+C \int e^{-x}\cos x \, dx = -\frac{1}{2} \left( e^{-x}\sin x – e^{-x}\cos x \right) + C

ここで、CC は積分定数です。

では、∫e−xcos⁡x dx\displaystyle\int e^{-x}\cos x \, dx も求めてみましょう。

まず、2つ目の微分式を整理します。

ddx(e−xcos⁡x)+ddx(e−xsin⁡x)=(−e−xsin⁡x–e−xcos⁡x)+(−e−xsin⁡x+e−xcos⁡x) \frac{d}{dx} \left( e^{-x}\cos x \right) + \frac{d}{dx} \left( e^{-x}\sin x \right) = \left( -e^{-x}\sin x – e^{-x}\cos x \right) + \left( -e^{-x}\sin x + e^{-x}\cos x \right)

=−2e−xsin⁡x = -2e^{-x}\sin x

次に、得られた式を両辺積分します。

∫ddx(e−xcos⁡x)+ddx(e−xsin⁡x) dx=∫−2e−xcos⁡x dx \int \frac{d}{dx} \left( e^{-x}\cos x \right) + \frac{d}{dx} \left( e^{-x}\sin x \right) \, dx = \int -2e^{-x}\cos x \, dx

左辺は、積分と微分が打ち消し合うため、元の関数が得られます。

e−xcos⁡x+e−xsin⁡x=∫−2e−xsin⁡x dx e^{-x}\cos x + e^{-x}\sin x = \int -2e^{-x}\sin x \, dx

したがって、積分結果は次のように表されます。

∫e−xsin⁡x dx=−12(e−xcos⁡x+e−xsin⁡x)+C \int e^{-x}\sin x \, dx = -\frac{1}{2} \left( e^{-x}\cos x + e^{-x}\sin x \right) + C

ここで、CC は積分定数です。

4. グラフ

ふゅか
ふゅか
e−xsin⁡xe^{-x}\sin x のグラフを書いてみましょう！

4.1. 極値

f′(x)=−e−xsin⁡x+e−xcos⁡x f'(x) = -e^{-x}\sin x + e^{-x}\cos x

極値を求めるためには、導関数がゼロになる点を求めます。

f′(x)=e−x(−sin⁡x+cos⁡x)=0 f'(x) = e^{-x} ( -\sin x+\cos x) = 0

ここで、e−x e^{-x} は常に正の値なので、極値は次の条件を満たす x x で生じます。

−sin⁡x+cos⁡x=0 -\sin x+\cos x = 0

三角関数の合成を行うと次のようになります。

2sin⁡(x+34π)=0 \sqrt{2} \sin\left(x + \frac{3}{4}\pi\right) = 0

したがって、xxは次のようになります。

x+34π=nπ(n∈Z) x + \frac{3}{4}\pi = n\pi \quad (n \in \mathbb{Z})

x=nπ–34π(n∈Z) x = n\pi – \frac{3}{4}\pi \quad (n \in \mathbb{Z})

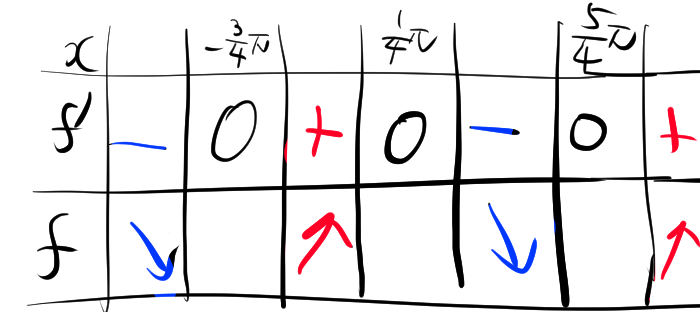
増減表は次のように書くことができます。

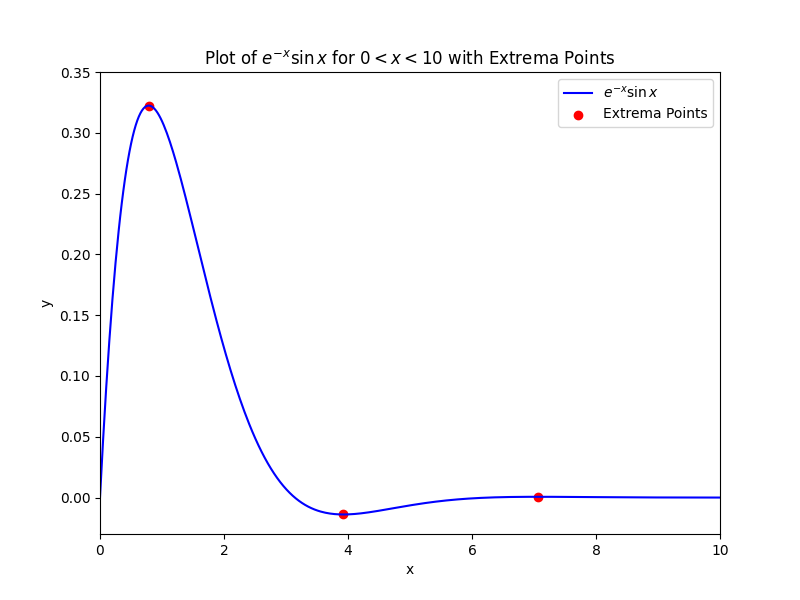
4.2. グラフ

グラフをプロットすると次のようになります。赤い点は極値です。

PR
ホームに戻る