極座標と直交座標の変換の具体例・例題について

1. 極座標とは
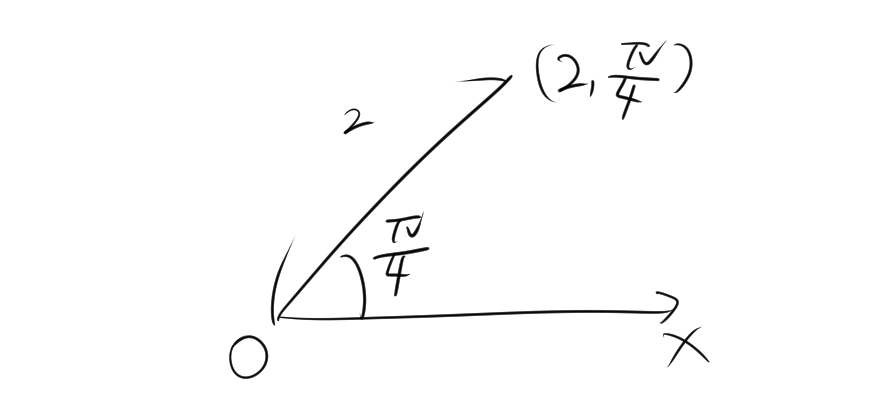
極座標は、平面上の任意の点を、原点からの距離(半径)と、原点からの角度で表す座標系です。
1.1. 極座標上の点
- 距離 \(r\): 原点から点 \(P\) までの距離。 \(r \geq 0\) 。
- 角度 \(\theta\): 始線(通常は正の \(x\) 軸)から、原点を中心として点 \(P\) まで測った反時計回りの角度。単位はラジアンや度が使われます。
例えば、点 \(P\) が原点から距離 \(r = 2\)、角度 \(\theta = \frac{\pi}{4}\) の位置にある場合、その極座標は \(P(2, \frac{\pi}{4})\) です。
2. 座標変換
2.1. 極座標から直交座標への変換
\[ x = r \cos \theta \]
\[ y = r \sin \theta \]
2.2. 極座標から直交座標への変換
\[ r = \sqrt{x^2 + y^2} \]
$$\cos\theta = \frac{x}{r}$$
$$\sin\theta = \frac{x}{r}$$
$\cos\theta$と$\sin\theta$から$\theta$を求めます。また、$\theta$は逆三角関数を利用すると、
\[ \theta = \tan^{-1} \left(\frac{y}{x}\right) \]
3. 例題
3.1. 例題1: 極座標から直交座標への変換
与えられた極座標は \( r = 5 \) と \( \theta = \frac{\pi}{4} \) より、
\( x \) 座標を求めます。
\[ x = 5 \cos\left(\frac{\pi}{4}\right) = 5 \times \frac{\sqrt{2}}{2} = \frac{5\sqrt{2}}{2} \]
\( y \) 座標を求めます。
\[ y = 5 \sin\left(\frac{\pi}{4}\right) = 5 \times \frac{\sqrt{2}}{2} = \frac{5\sqrt{2}}{2} \]
したがって、点 \( P \) の直交座標は \( \left( \frac{5\sqrt{2}}{2}, \frac{5\sqrt{2}}{2} \right) \) です。
3.2. 例題2: 直交座標から極座標への変換
与えられた直交座標は \( x = 3 \) と \( y = 3\sqrt{3} \) です。
\( r \) を求めます。
\[ r = \sqrt{3^2 + (3\sqrt{3})^2} = \sqrt{9 + 27} = \sqrt{36} = 6 \]
\( \theta \) を求めます。
$$\sin \theta = \frac{x}{r} = \frac{3}{6}=\frac{1}{2}$$
$$\cos \theta = \frac{y}{r} = \frac{3\sqrt{3}}{6}=\frac{\sqrt{3}}{2}$$
$\theta=\frac{\pi}{3}$である。したがって、点 \( Q \) の極座標は \( (r, \theta) = (6, \frac{\pi}{3}) \) です。
また、逆三角関数を利用して、次のように求めることができる。
\[ \theta = \tan^{-1}\left(\frac{3\sqrt{3}}{3}\right) = \tan^{-1}(\sqrt{3}) \]
\( \tan^{-1}(\sqrt{3}) = \frac{\pi}{3} \) なので、\( \theta = \frac{\pi}{3} \)