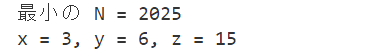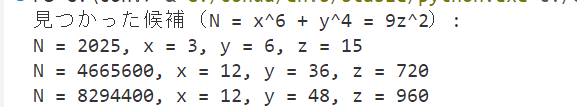京都大学（理系）2025年度数学第2問解答解説

問題はご自身で探してください。

1. 解説

3を法としたとき、ある整数kが3で割り切れないときに、合同式は

$$k^2 \equiv (\pm 1)^2 \equiv 1 \pmod{3}$$

したがって、$k^6 = (k^2)^3 \equiv 1^3 \equiv 1 \pmod{3}$ および $k^4 = (k^2)^2 \equiv 1^2 \equiv 1 \pmod{3}$ です。

もし $x$ と $y$ の両方が3で割り切れなければ、$x^6 \equiv 1,\quad y^4 \equiv 1$となるので

$$x^6+y^4\equiv 2 \pmod{3}$$

一方、右辺 $9z^2$ は3の倍数であるため、

$$9z^2\equiv 0 \pmod{3}$$

よって合同式は成立せず、少なくとも $x$ と $y$ のいずれも、もしくは両方とも3の倍数でなければならないことが分かります。

また、片方だけが3の倍数の場合も合同式は成立しないので、$x$ と $y$ は必ず3の倍数でなければなりません。

$x$ と $y$ が3の倍数であることから、

a,bを任意の正の整数として、$x = 3a,\quad y = 3b$と置きます。

$$x^6 = (3a)^6 = 3^6a^6 = 729a^6,\quad y^4 = (3b)^4 = 3^4b^4 = 81b^4$$

これを元の式に代入すると、

$$729a^6 + 81b^4 = 9z^2$$

両辺を9で割ると、 $$81a^6 + 9b^4 = z^2 \tag{1}$$

式 (1) の右辺 $z^2$ は左辺が9の倍数であることから、$z$ も3の倍数と考えられます。

よって、ｃを任意の正の整数として、$z = 3c$ と置くと、$z^2 = 9c^2$ となります。

式 (1) に代入し、 $$81a^6 + 9b^4 = 9c^2$$

両辺をさらに9で割ると、

$$9a^6 + b^4 = c^2 \tag{2}$$

$a\geq 1,b\geq 1$より、$c^2\geq 10$であることがわかります。cが整数になるように小さい平方数から試していきます。

[1]$c^2=16$であるとき、

$$9a^6 + b^4 =16$$

a=1であるとき、$b^4=7$となるので不適。

a>1では、$b^4<0$となるので不適。

[2]$c^2=25$であるとき、

$$9a^6 + b^4 =25$$

a=1であるとき、$b^4=16$となるので$b=2$。

したがって、求める $N$ は$z=3\times 5=15$のときであるから、

$$N = 9z^2 = 9\cdot15^2 = 9\cdot225 = 2025$$

正の整数 $N$ の最小値は 2025 である。

aが明らかに大きくなることに着目するのが重要ですね。昔に3を法とする整数問題があったような。

2. 補足

式 (2) $$c^2 = 9a^6 + b^4$$ の最も小さい正の整数解を求めるため、まず $a = 1$ と置いて、代入して求めることもできます。すると、 $$c^2 = 9\cdot1^6 + b^4 = 9 + b^4.$$ $b$ の最小値は1ですが、

• $b = 1$ のとき：$c^2 = 9 + 1 = 10$ となり平方数ではありません。
• $b = 2$ のとき：$c^2 = 9 + 16 = 25$ となり、これは平方数で $c = 5$ です。

したがって、

$$a = 1,\quad b = 2,\quad c = 5.$$

置換 $x = 3a,\; y = 3b,\; z = 3c$ より、

$$x = 3,\quad y = 6,\quad z = 15.$$

3. 関連

任意の正の整数 $k$ について、$k$ が3で割り切れないとき、フェルマーの小定理から

$$k^2 \equiv 1 \pmod{3}$$

が成り立つことがわかります。

4. プログラムから見た問題

4.1. 方針

• 小さな $x, y$ の組み合わせについて、 $x^6 + y^4$ を計算する。
• それが 9で割り切れる（すなわち、$N = x^6 + y^4$ が9の倍数）なら、 $$z^2 = \frac{x^6 + y^4}{9}$$ を求め、これが平方数（＝整数の2乗）なら、候補として採用。
• 候補の中から、最小の $N = 9z^2$ を選ぶ。

4.2. Python コード

import math

# 最小値探索用の初期値（十分大きく）
min_N = float('inf')
min_x = min_y = min_z = None

# 探索範囲（x, y が小さい方が N も小さくなる可能性が高い）
for x in range(1, 100):
    x6 = x ** 6
    for y in range(1, 100):
        y4 = y ** 4
        total = x6 + y4

        if total % 9 != 0:
            continue  # 9で割れないなら無視

        z_squared = total // 9
        z = int(math.isqrt(z_squared))
        if z * z == z_squared:  # z² が完全平方数か？
            N = 9 * z_squared
            if N < min_N:
                min_N = N
                min_x, min_y, min_z = x, y, z

print(f"最小の N = {min_N}")
print(f"x = {min_x}, y = {min_y}, z = {min_z}")

4.3. 出力結果

4.4. 2025以外の解の候補

import math

results = []

# 適度な範囲で探索（大きくすると時間がかかる）
for x in range(1, 50):
    x6 = x ** 6
    for y in range(1, 50):
        y4 = y ** 4
        total = x6 + y4

        if total % 9 != 0:
            continue  # 9で割り切れないものは無視

        z_squared = total // 9
        z = int(math.isqrt(z_squared))
        if z * z == z_squared:  # 完全平方数ならOK
            N = 9 * z_squared
            results.append((N, x, y, z))

# N の小さい順にソートして表示
results.sort()

print("見つかった候補（N = x^6 + y^4 = 9z^2）:")
for N, x, y, z in results[:10]:  # 最初の10個
    print(f"N = {N}, x = {x}, y = {y}, z = {z}")