【論理回路】NOR回路の真理値表と論理式・回路の構成について

1. NOR回路
NOR回路(否定論理和回路)は、OR回路の出力を否定(反転)したものです。入力信号のいずれかが「1」(High、真)であれば出力が「0」(Low、偽)となり、すべての入力信号が「0」の場合のみ出力が「1」になります。
つまり、「OR回路の否定をとる回路」と考えることができます。
2. NOR回路の真理値表
2入力のOR回路とNOR回路における真理値表です。
| 入力A | 入力B | OR | NOR |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
- 入力A、入力B: NORゲートに加えられる2つの入力信号。
- OR: OR回路の出力。少なくとも1つの入力が1であれば1。
- NOR: OR回路の出力を否定したもの。
3. NOR回路の論理式
3.1. 論理式
$Y$をNOR回路の出力とすると、OR回路の否定となるので、論理式は次のようになります。
\[Y= \overline{A + B}\]
3.2. MIL記号
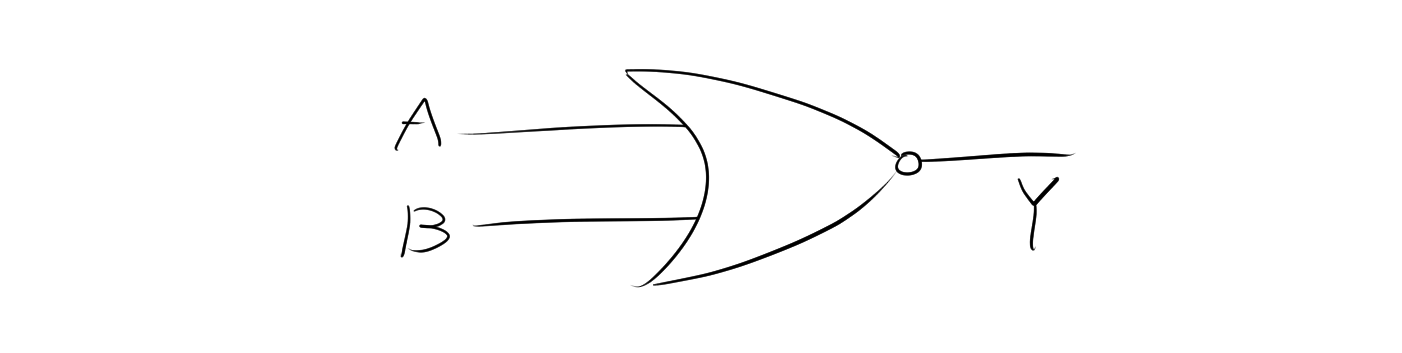
以下は、2入力NOR回路のMIL記号です。
3.3. 回路図
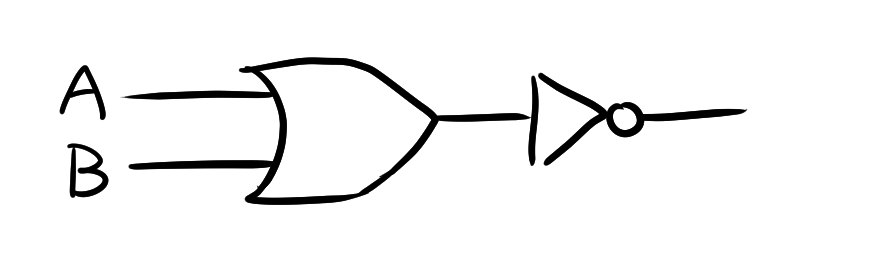
$Y= \overline{A + B}$であることから、NOR回路はOR回路のNOT回路で次のように回路図を書くことができます。
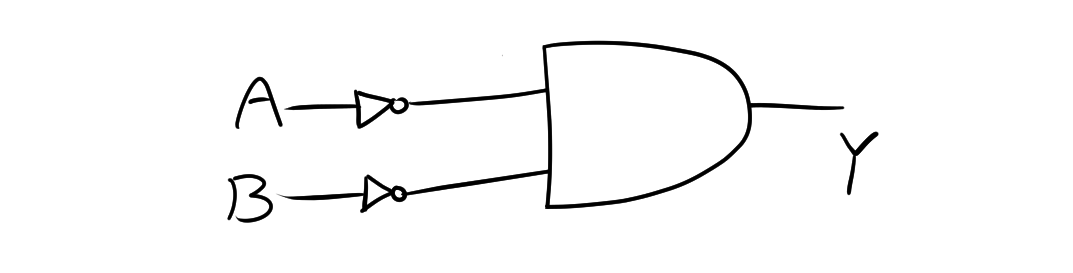
 一方で、$Y= \overline{A}\cdot \overline {B}$であることから、NOR回路はAND回路のNOT回路で次のように回路図を書くことができます。
一方で、$Y= \overline{A}\cdot \overline {B}$であることから、NOR回路はAND回路のNOT回路で次のように回路図を書くことができます。
4. 回路の構成
4.1. NOT回路の構成
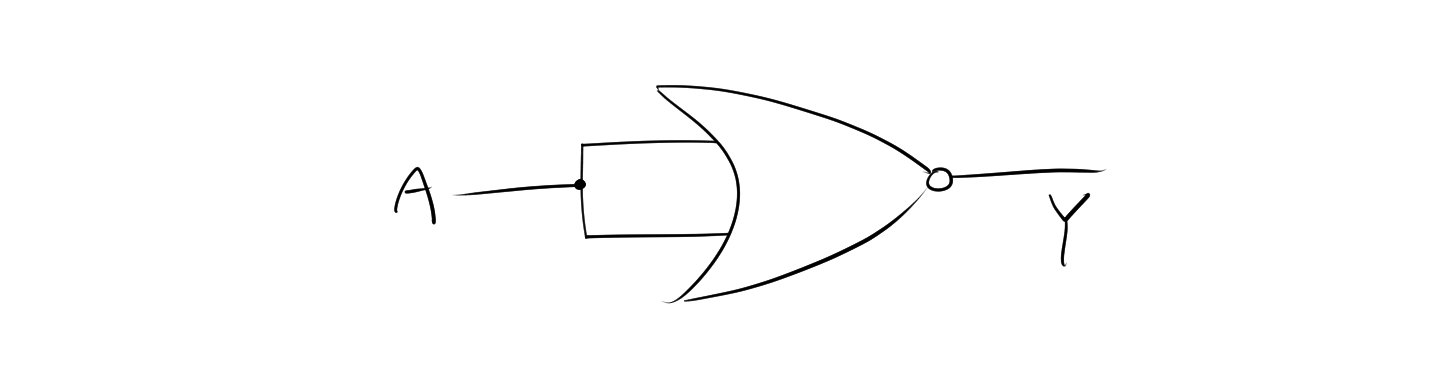
NOT回路は、1つの入力信号を受け取り、その信号を反転します。入力が1なら出力は0、入力が0なら出力は1です。NOR回路を用いて論理式は次のようになります。
\[Y= \overline{A}= \overline{A + A}\]
したがって、回路図は次のようになります。
4.2. OR回路の構成
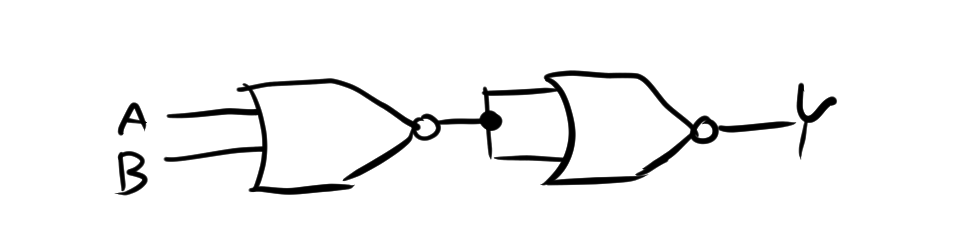
OR回路は、入力信号を受け取り、それらの論理和(OR)を出力します。論理式は次のようになります。
\[Y=A+B= \overline{\overline{A + B}}= \overline{\overline{A + B}+\overline{A + B}}\]
したがって、回路図は次のようになります。
4.3. AND回路の構成
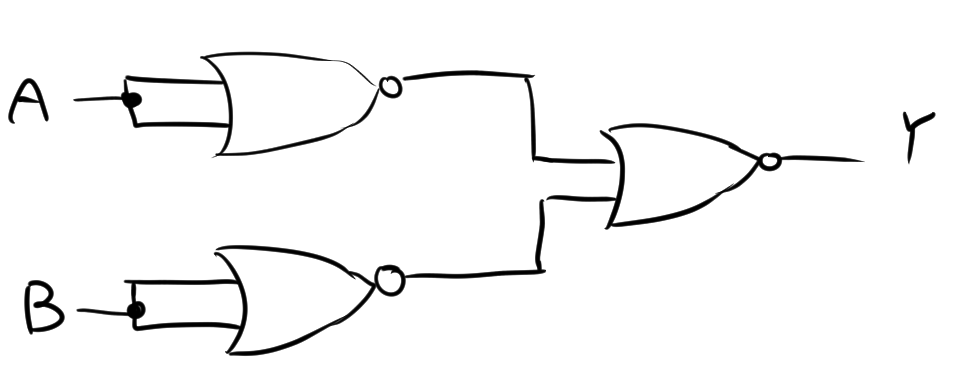
AND回路もNOR回路を3つ組み合わせて作れます。論理式は次のようになります。
\[\begin{align*}Y &= A\cdot B \\ &= \overline{\overline{A\cdot B}} \\ &= \overline{\overline{A}+ \overline{B}} \\ &= \overline{\overline{A + A}+ \overline{B+B}} \\ \end{align*}\]
したがって、回路図は次のようになります。