UCS(均一コスト探索）について解説！経路探索の例付き

はるか

今日はUCS（均一コスト探索）について話すよ。

ふゅか

いいね！UCSってどういうアルゴリズムなの？

1. UCSとは？

UCSとは日本語で均一コスト探索と呼ばれる、経路探索のアルゴリズムである。UCSはbest-first search（最良優先探索）の一種と考えることができる。best-first searchとは評価関数f(n)の中から一番いいやつを選択するsearchである。

ふゅか

best-first searchの一種なんだね。評価関数f(n)で一番良いノードを選ぶんでしょ？

はるか

そうだよ。評価関数f(n)は始点からノードnまでの累積コストなんだ。

2. UCSの評価関数

UCSの評価関数は、現在のノードからの累積コストである。具体的には、評価関数$f(n)$は、始点からノード$n$までのコストである$g(n)$であり、次のように表される。

$f(n) = g(n)$

ここで、$g(n)$ は始点からノード$n$までの実際にかかった経路コストを表す。

2.1. UCSの経路探索の例

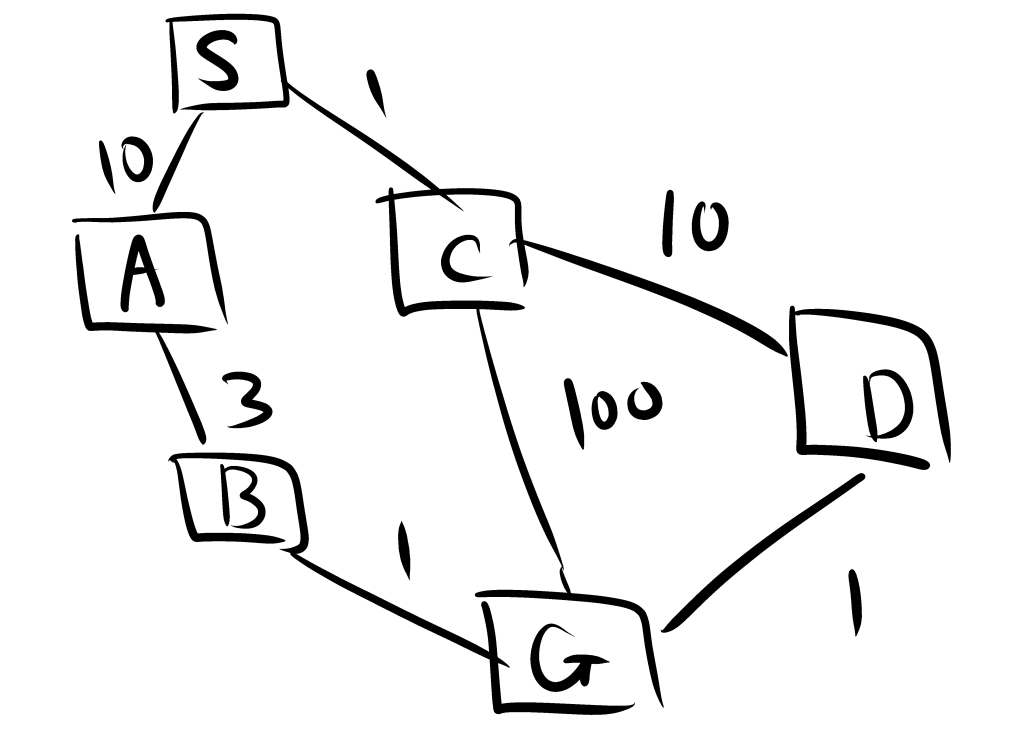
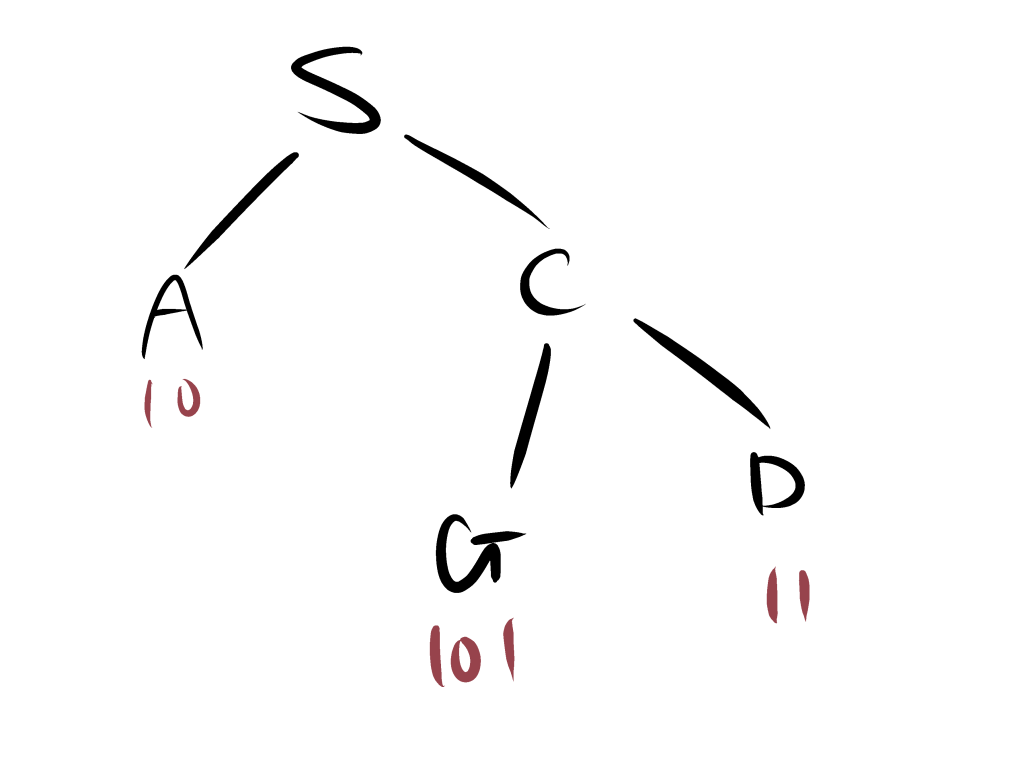
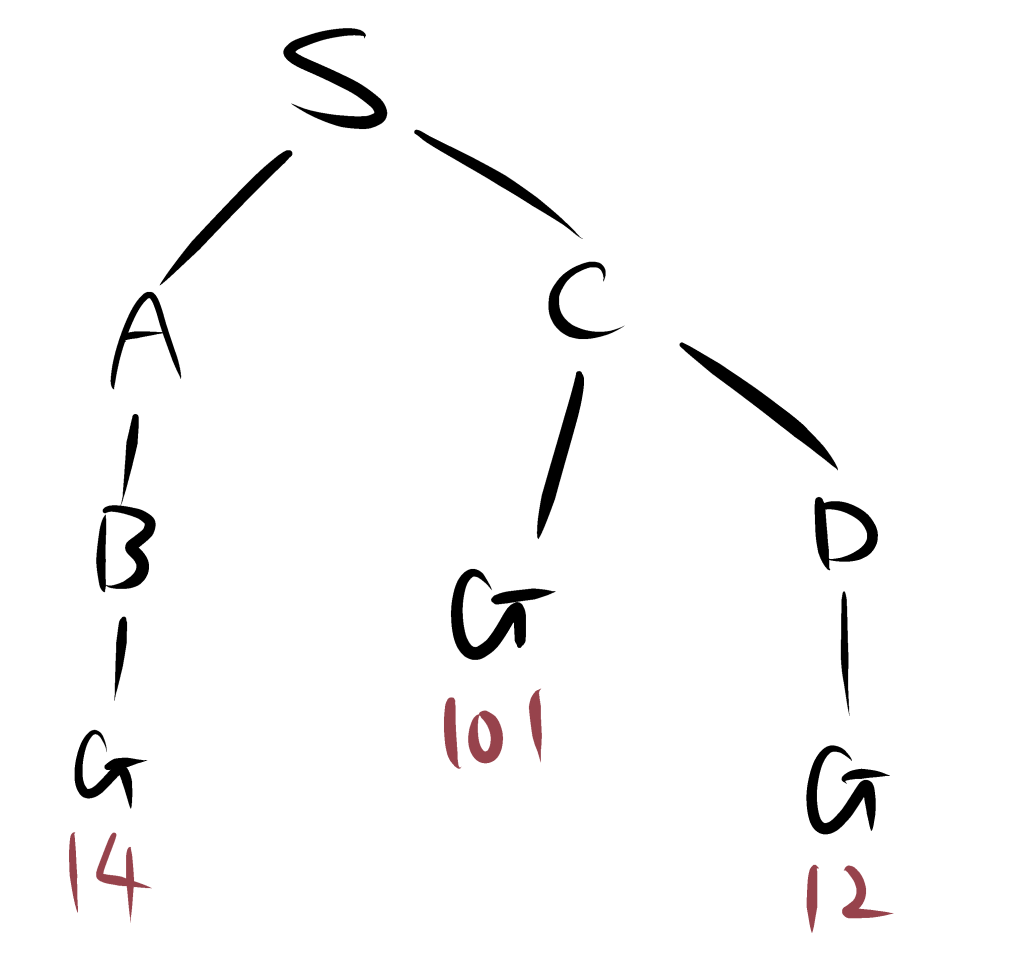
SからGまでの経路をUCSで求める。

評価関数が小さい順にノードを木構造で展開する。

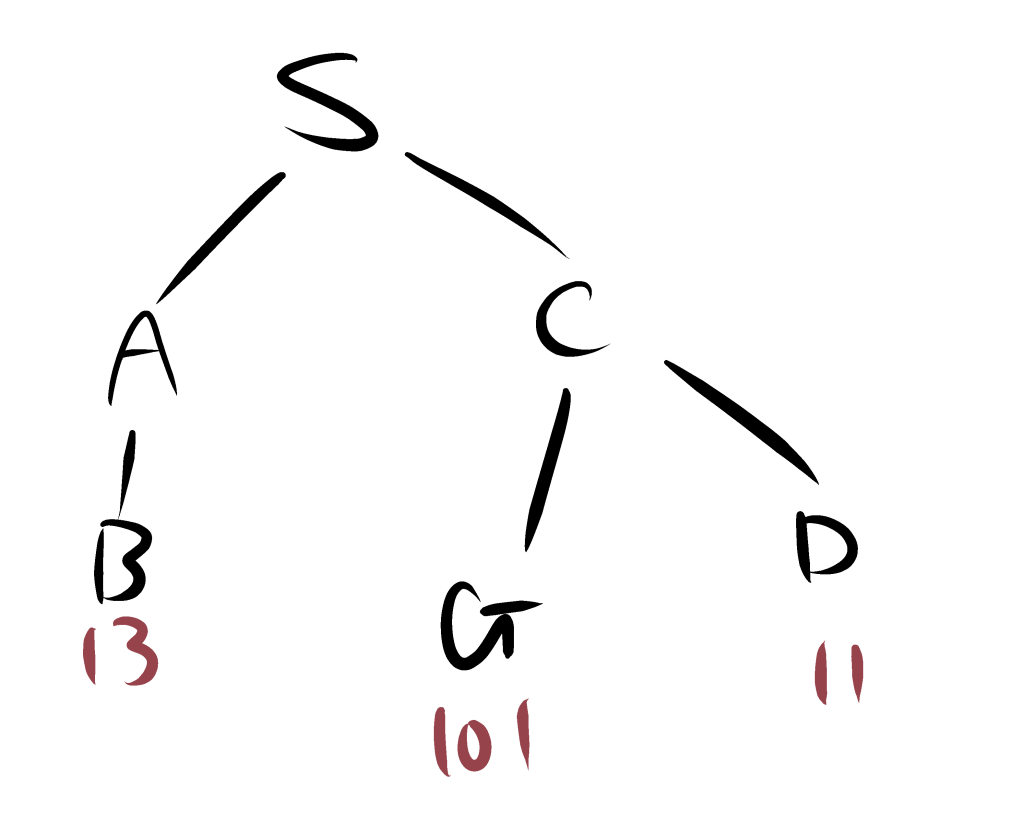
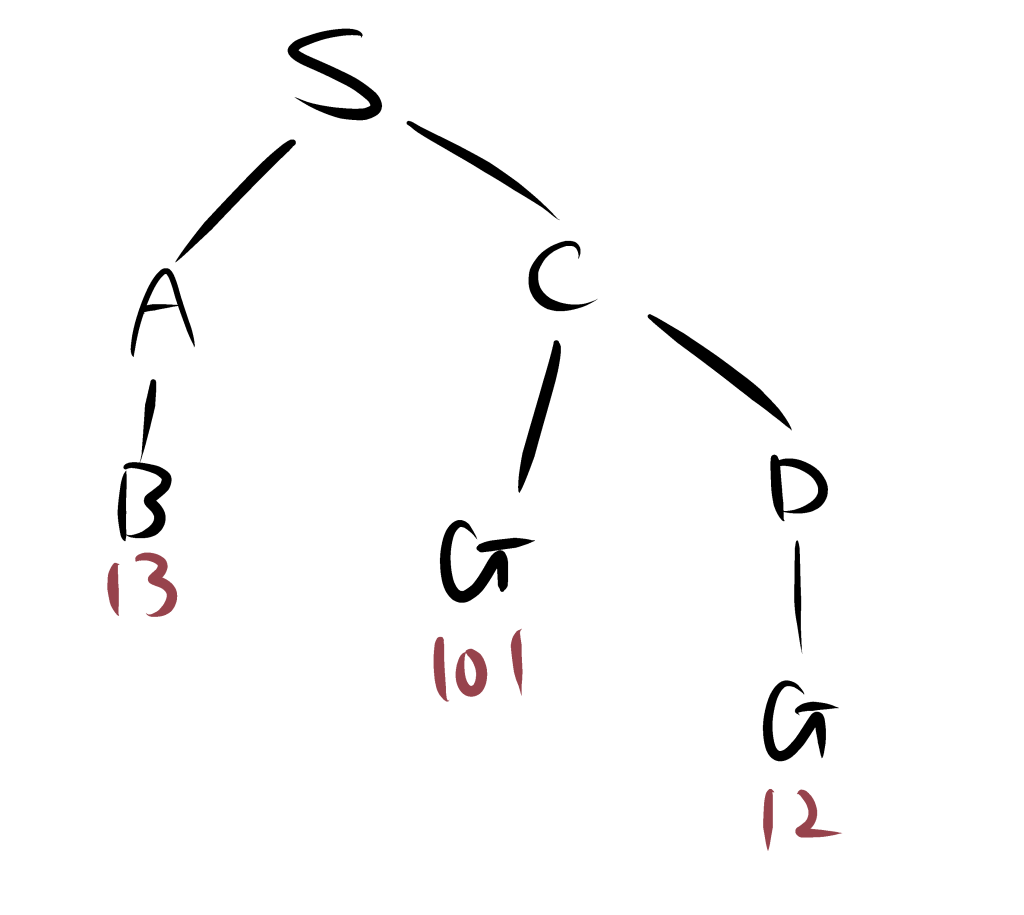
このことから、S-C-D-Gが最適な経路であることがわかる。
Bは展開しなくても、S-C-D-Gが最適な経路であることはわかりますが、一応展開すると以下のようになる。

3. UCSの性質

3.1. UCSの計算時間

$C^{*}$を最適コスト、$b$を各ノードからの子ノードの数（分岐数）とする。

目的地までのコストが$C^{*}$で、各ステップでゴールに、$\epsilon$ずつ近づく場合、必要なステップ数は次のように表されます。

$step=\left\lfloor\dfrac{C^{*}}{\epsilon}\right\rfloor + 1$

したがって、探索に必要なノード展開数は以下のようになる。

$O(b^{step})=O(b^{\left\lfloor\frac{C^{*}}{\epsilon}\right\rfloor + 1})$