【図解】相加相乗平均の証明と例題について

1. 2変数の相加相乗平均
$a\geqq0,b\geqq0$のとき、
$$\dfrac{a+b}{2}\geqq\sqrt{ab}$$
等号成立条件は$a=b$の時である。
2. 相加相乗平均の証明
2.1. 計算して相加相乗平均を証明する
まず、$a \geq 0$、$b \geq 0$ であるとき、次の式を考えます。
$$a + b – 2\sqrt{ab} = \left(\sqrt{a} – \sqrt{b}\right)^{2} \geqq 0$$
この結果、次のような不等式が導かれます。
$$\begin{align*} a + b &\geqq 2 \sqrt{ab} \\ \therefore\ \dfrac{a + b}{2} &\geqq \sqrt{ab} \end{align*}$$
$\therefore\dfrac{a+b}{2}\geqq\sqrt{ab}$
また、等号成立条件は
$$\left(\sqrt{a}-\sqrt{b}\right)^{2}= 0$$
より、$a=b$のときである。
3. 相加相乗平均の視覚化
円と線分を使って、相加相乗平均を視覚的に理解する方法を紹介します。
まず、$o$を中心とする円を描きます。視覚的に、$\sqrt{ab}$と$\frac{a+b}{2}$の大小関係がわかります。一方で、この円の直径と垂直に交わる線分が$\sqrt{ab}$である理由を考えてみます。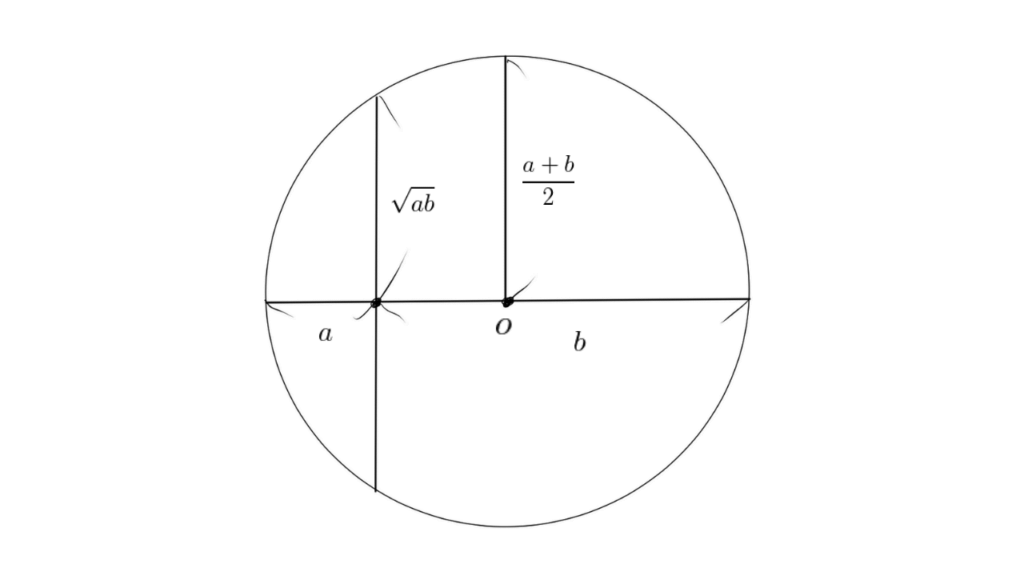
3.1. 方べきの定理を用いた証明
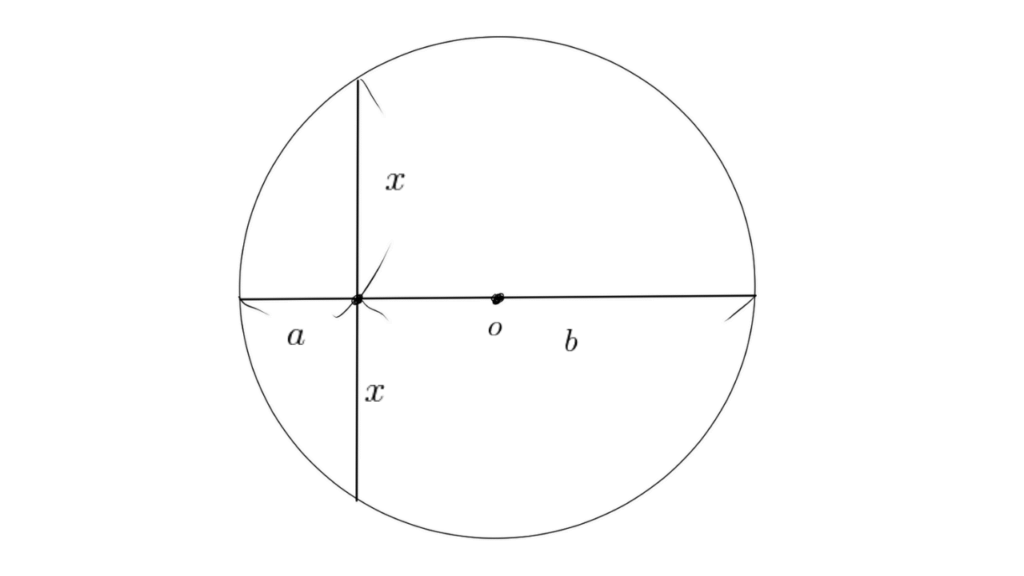
$x > 0$ のとき、方べきの定理により次の式が成り立ちます。
$$\begin{align*} x^2 &= ab \\ \therefore\ x &= \sqrt{ab} \end{align*}$$
3.2. 三平方の定理を用いた証明
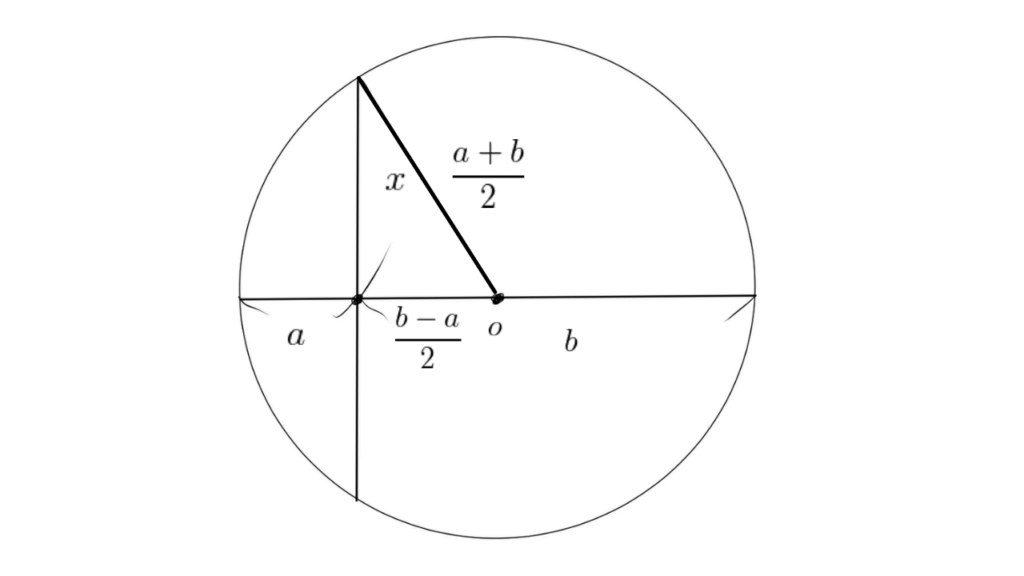
$x > 0$ のとき、三平方の定理を用いて次のように証明します。
$$\begin{align*} x^{2} &= \left( \dfrac{a+b}{2}\right) ^{2}-\left( \dfrac{b-a}{2}\right) ^{2} \\ x^{2} &= \dfrac{a^{2}+2ab+b^{2}-\left( a^{2}-2ab+b^{2}\right) }{4} \\ \Leftrightarrow\ x^{2} &= ab \\ \therefore\ x &= \sqrt{ab} \end{align*} $$
4. 相加相乗平均の例題
4.1. 例題1
相加相乗平均の不等式より、
\[ x + \dfrac{9}{x} \geq 2\sqrt{x \cdot \dfrac{9}{x}} = 2\sqrt{9} = 6 \]
等号が成立するのは \( x = \dfrac{9}{x} \) のとき、すなわち \( x^2 = 9 \) であり、\( x > 0 \) より \( x = 3 \)。
したがって、最小値は 6 で、\( x = 3 \) のときに等号が成立する。
4.2. 例題2
まず、\( x > 2 \) より \( x – 2 > 0 \)。相加相乗平均の不等式を \( x – 2 \) と \( \dfrac{9}{x – 2} \) に適用すると、
\[2+ (x – 2) + \dfrac{9}{x – 2} \geq 2+2\sqrt{(x – 2) \cdot \dfrac{9}{x – 2}} = 2+2\sqrt{9} = 8 \]
等号が成立するのは \( x – 2 = \dfrac{9}{x – 2} \) のとき、すなわち \( (x – 2)^2 = 9 \) であり、\( x – 2 > 0 \) より \( x – 2 = 3 \)、したがって \( x = 5 \)。
最小値は 8 で、\( x = 5 \) のときに等号が成立する。
4.3. 例題3
まず、式を展開する
\[ \left( x + \dfrac{2}{x} \right) \left( x + \dfrac{1}{x} \right) = x^2 + x \cdot \dfrac{1}{x} + \dfrac{2}{x} \cdot x + \dfrac{2}{x} \cdot \dfrac{1}{x} = x^2 + 1 + 2 + \dfrac{2}{x^2} \]
まとめると、
\[ x^2 + \dfrac{2}{x^2} + 3 \]
ここで、\( x > 0 \) なので相加相乗平均の不等式を \( x^2>0 \) と \( \dfrac{2}{x^2} >0 \) に適用すると、
\[ x^2 + \dfrac{2}{x^2} \geq 2\sqrt{x^2 \cdot \dfrac{2}{x^2}} = 2\sqrt{2} = 2\sqrt{2} \]
したがって、
\[ x^2 + \dfrac{2}{x^2} + 3 \geq 2\sqrt{2} + 3 \]
最小値は \( 3 + 2\sqrt{2} \) で、等号が成立するのは \( x^2 = \dfrac{2}{x^2} \)、すなわち \( x^4 = 2 \) のとき。\( x > 0 \) より \( x = \sqrt[4]{2} \)。
4.3.1. 注意
$$ \left( x + \dfrac{2}{x} \right) \left( x + \dfrac{1}{x} \right) $$に対して、それぞれの相加相乗平均を考えると、
$$ \left( x + \dfrac{2}{x} \right)\geqq 2\sqrt{2} $$
$$ \left( x + \dfrac{1}{x} \right)\geqq 2 $$
として、最小値はその積
$$ \left( x + \dfrac{2}{x} \right) \left( x + \dfrac{1}{x} \right)\geqq 4\sqrt{2} $$
とするのは間違いです。なぜなら、等号成立条件がそれぞれ $ x= \sqrt 2, x= 1$となるので、等号が成り立つとき、つまり最小値は$4\sqrt{2}$になることはありません。このことから、等号成立条件をチェックする必要性があることがわかります。
4.4. 例題4
まず、\( x > \sqrt{2} \) より、\( x^2 – 2 > 0 \) となり、分母は定義されます。
変数変換として、\( t = \sqrt{x^2 – 2} \) と置きます。すると、\( t > 0 \) です。
このとき、
\[ t^2 = x^2 – 2 \]
\[ x^2 = t^2 + 2 \]
これを元の式に代入すると
\[ \dfrac{x^2 + 9}{\sqrt{x^2 – 2}} = \dfrac{(t^2 + 2) + 9}{t} = \dfrac{t^2 + 11}{t} = t + \dfrac{11}{t} \]
したがって、問題は \( f(t) = t + \dfrac{11}{t} \) の最小値を求めることに帰着されます。ただし、\( t > 0 \) です。
相加相乗平均の不等式より、
\[ t + \dfrac{11}{t} \geq 2\sqrt{t \cdot \dfrac{11}{t}} = 2\sqrt{11} \]
等号が成立するのは、
$$\begin{align*} t &= \dfrac{11}{t} \\ t^2 &= 11 \\ t &= \sqrt{11} \end{align*}$$
(\( t > 0 \) より)
元の変数 \( x \) に戻すと、
\[\begin{align*} \sqrt{x^2 – 2} &= \sqrt{11} \\ x^2 – 2 &= 11 \\ x^2 &= 13 \\ x &= \sqrt{13} \end{align*} \]
(\( x > \sqrt{2} \) より、\( x = \sqrt{13} \))
最小値は、
\[ f(t) = t + \dfrac{11}{t} = \sqrt{11} + \dfrac{11}{\sqrt{11}} = \sqrt{11} + \sqrt{11} = 2\sqrt{11} \]
したがって、求める最小値は \( 2\sqrt{11} \) であり、\( x = \sqrt{13} \) のときに等号が成立する。
5. 相加相乗平均の一般化
$a_{i}\ (i=1.2.3\cdots\ n)$が$a_{i}>0$を満たすとき、
$\Large\dfrac{1}{n}\sum \limits ^{n}_{i=1}a_{i}\geq \sqrt[n] {\prod\limits ^{n}_{i=1}a_{i}} $
$\dfrac{a_{1}+a_{2}+…+a_{n}}{n}\geq \sqrt[n] {a_{1}a_{2}\ldots a_{n}}$
具体的に書くとこうなります。
となる。
等号成立条件は$a_{1}=a_{2}=a_{3}=\cdots=a_{n}$となる。これはAM-GM不等式とも呼ばれています。





