ベータ分布の意味と期待値・分散の導出について

「0から1の間で、特定の範囲にデータが集まりやすい確率分布はないのか?」
確率論や統計学に興味を持ち始めたとき、多くの人がこの疑問を抱きます。
例えば、ある製品の不良率や、A/Bテストの成功確率を考える際に登場するのが ベータ分布 です。
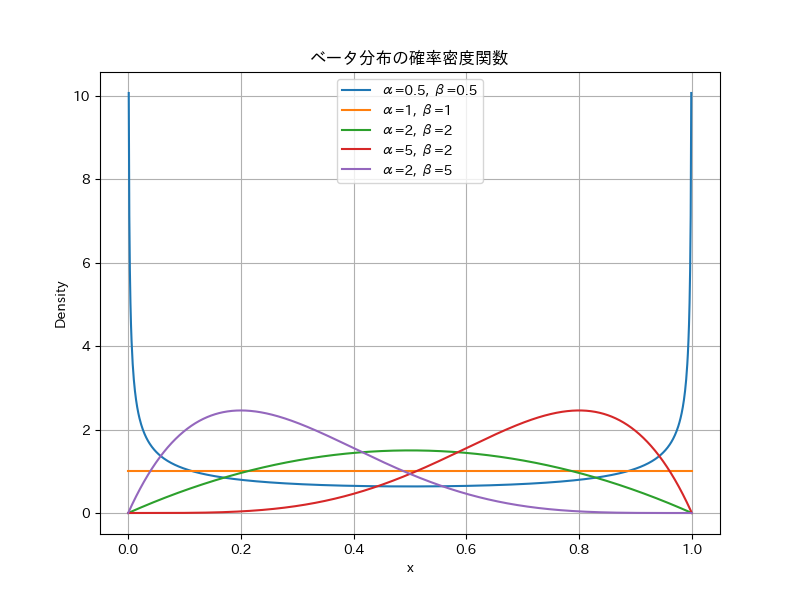
1. ベータ分布とは
ベータ分布は、区間 \([0,1]\) 上で定義される確率分布です。確率密度関数 (PDF) は、以下の式で与えられます:
\[ \text{Beta}(x \mid \alpha, \beta) = \frac{x^{\alpha – 1} (1 – x)^{\beta – 1}}{\mathrm{B}(\alpha, \beta)}, \quad 0 \le x \le 1 \]
ここで、\(\alpha > 0\) と \(\beta > 0\) は形状パラメータ (shape parameters) であり、\(\mathrm{B}(\alpha, \beta)\) はベータ関数です。ベータ関数 \(\mathrm{B}(\alpha, \beta)\) は以下のように定義されます。
\[ \mathrm{B}(\alpha, \beta) = \int_0^1 t^{\alpha – 1} (1-t)^{\beta – 1} \, dt = \frac{\Gamma(\alpha)\,\Gamma(\beta)}{\Gamma(\alpha + \beta)}\]
\(\Gamma(\cdot)\) はガンマ関数です。
2. 期待値・分散
ベータ分布の期待値 (mean) と分散 (variance) は、それぞれ以下のように表せます。
期待値: \[ E[X] = \frac{\alpha}{\alpha + \beta} \]
分散: \[ \mathrm{Var}(X) = \frac{\alpha \beta}{(\alpha + \beta)^2 (\alpha + \beta + 1)} \]
これらの式から、\(\alpha\) と \(\beta\) の比によって分布の中心や広がりが決まることがわかります。
2.1. 期待値の導出
期待値 \(E[X]\) は、次の積分で求めます:
\[ E[X] = \int_0^1 x f(x) \, dx \]
PDF を代入すると、
\[ E[X] = \int_0^1 x \cdot \frac{x^{\alpha – 1} (1 – x)^{\beta – 1}}{\mathrm{B}(\alpha, \beta)} \, dx \]
\[ = \frac{1}{\mathrm{B}(\alpha, \beta)} \int_0^1 x^{\alpha} (1 – x)^{\beta – 1} \, dx \]
ここで、ベータ関数の性質
\[ \int_0^1 t^{m-1} (1 – t)^{n-1} \, dt = \mathrm{B}(m, n) = \frac{\Gamma(m) \Gamma(n)}{\Gamma(m+n)} \]
を利用すると、上の積分部分はベータ関数 \(\mathrm{B}(\alpha+1, \beta)\) に対応します:
\[ E[X] = \frac{\mathrm{B}(\alpha + 1, \beta)}{\mathrm{B}(\alpha, \beta)} \]
\(\mathrm{B}(\alpha, \beta)\) のガンマ関数表示を使って変形すると、
\[ \mathrm{B}(\alpha + 1, \beta) = \frac{\Gamma(\alpha + 1) \Gamma(\beta)}{\Gamma(\alpha + \beta + 1)} \]
\[ \mathrm{B}(\alpha, \beta) = \frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha + \beta)} \]
これらの比をとると、
\[ E[X] = \frac{\Gamma(\alpha + 1) \Gamma(\beta) \Gamma(\alpha + \beta)}{\Gamma(\alpha) \Gamma(\beta) \Gamma(\alpha + \beta + 1)} \]
ここで、ガンマ関数の性質 \(\Gamma(z+1) = z\Gamma(z)\) を使うと、
\[ \Gamma(\alpha + 1) = \alpha \Gamma(\alpha) \]
を代入して、
\[ E[X] = \frac{\alpha \Gamma(\alpha) \Gamma(\beta) \Gamma(\alpha + \beta)}{\Gamma(\alpha) \Gamma(\beta) (\alpha + \beta) \Gamma(\alpha + \beta)} \]
\(\Gamma(\alpha)\), \(\Gamma(\beta)\), \(\Gamma(\alpha + \beta)\) を約分すると、
\[ E[X] = \frac{\alpha}{\alpha + \beta} \]
2.2. 分散の導出
分散 \(\text{Var}(X)\) は、次の式で求めます。
\[ \text{Var}(X) = E[X^2] – (E[X])^2 \]
まず、\(E[X^2]\) を求めます。
\[ E[X^2] = \int_0^1 x^2 f(x) \, dx \]
\[ = \int_0^1 x^2 \cdot \frac{x^{\alpha – 1} (1 – x)^{\beta – 1}}{\mathrm{B}(\alpha, \beta)} \, dx \]
\[ = \frac{1}{\mathrm{B}(\alpha, \beta)} \int_0^1 x^{\alpha+1 – 1} (1 – x)^{\beta – 1} \, dx \]
ここで、ベータ関数の性質を再び利用すると、この積分は \(\mathrm{B}(\alpha+2, \beta)\) に等しくなります。
\[ E[X^2] = \frac{\mathrm{B}(\alpha + 2, \beta)}{\mathrm{B}(\alpha, \beta)} \]
\(\mathrm{B}(\alpha+2, \beta)\) をガンマ関数で表すと、
\[ \mathrm{B}(\alpha+2, \beta) = \frac{\Gamma(\alpha+2) \Gamma(\beta)}{\Gamma(\alpha+\beta+2)} \]
また、\(\Gamma(\alpha+2)\) の性質を用いて、
\[ \Gamma(\alpha+2) = (\alpha+1)\alpha\Gamma(\alpha) \]
を代入すると、
\[ E[X^2] = \frac{(\alpha+1)\alpha \Gamma(\alpha) \Gamma(\beta) \Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta) (\alpha+\beta)(\alpha+\beta+1) \Gamma(\alpha+\beta)} \]
約分して、
\[ E[X^2] = \frac{\alpha(\alpha+1)}{(\alpha+\beta)(\alpha+\beta+1)} \]
分散は
\[ \text{Var}(X) = E[X^2] – (E[X])^2 \]
\[ = \frac{\alpha(\alpha+1)}{(\alpha+\beta)(\alpha+\beta+1)} – \left(\frac{\alpha}{\alpha+\beta}\right)^2 \]
通分して整理すると、
\[ \text{Var}(X) = \frac{\alpha\beta}{(\alpha+\beta)^2 (\alpha+\beta+1)} \]
3. 期待値とディガンマ関数
ここで、\( \psi(\cdot) \) は ディガンマ関数 (digamma function) を表します。
3.1. 積分表示
期待値 \( E[\ln X] \) は定義より
\[ E[\ln X] = \int_{0}^{1} \ln(x)\, f(x)\, dx = \frac{1}{B(\alpha, \beta)} \int_{0}^{1} \ln(x)\, x^{\alpha – 1} (1 – x)^{\beta – 1}\, dx \]
と書けます。
3.2. ベータ関数の微分
ベータ関数 \( B(p,q) \) の定義
\[ B(p,q) = \int_{0}^{1} x^{p – 1} (1 – x)^{q – 1}\, dx \]
を用いて、変数 \(p\) に関する微分を考えます。
\[ \frac{\partial}{\partial p} B(p,q) = \frac{\partial}{\partial p} \int_{0}^{1} x^{p – 1} (1 – x)^{q – 1}\, dx = \int_{0}^{1} \frac{\partial}{\partial p} \bigl[x^{p – 1} (1 – x)^{q – 1}\bigr] dx \]
\( x^{p – 1} \) を \( p \) で微分すると \( x^{p-1} \ln(x) \) が出るため、結局
\[ \frac{\partial}{\partial p} B(p,q) = \int_{0}^{1} x^{p – 1} (1 – x)^{q – 1} \ln(x)\, dx \]
となります。これより、
\[ \int_{0}^{1} x^{p – 1} (1 – x)^{q – 1} \ln(x)\, dx = \frac{\partial}{\partial p} B(p,q) \]
3.3. 元の期待値への応用
先ほどの期待値に戻ると、
\[ E[\ln X] = \frac{1}{B(\alpha, \beta)} \int_{0}^{1} \ln(x)\, x^{\alpha – 1} (1 – x)^{\beta – 1}\, dx = \frac{1}{B(\alpha, \beta)} \frac{\partial}{\partial \alpha} B(\alpha, \beta) \]
したがって、あとは \( B(\alpha,\beta) \) の \(\alpha\) に関する微分を計算すればよいわけです。
3.4. ベータ関数とガンマ関数の関係
\[ B(\alpha,\beta) = \frac{\Gamma(\alpha)\,\Gamma(\beta)}{\Gamma(\alpha + \beta)} \]
両辺の対数をとると
\[ \ln B(\alpha, \beta) = \ln \Gamma(\alpha)+\ln \Gamma(\beta)-\ln \Gamma(\alpha + \beta)\]
\(\alpha\) で微分すると、
\[ \frac{\partial}{\partial \alpha} \ln B(\alpha, \beta) = \frac{\partial}{\partial \alpha} \ln \Gamma(\alpha)+0-\frac{\partial}{\partial \alpha} \ln \Gamma(\alpha + \beta) = \psi(\alpha) – \psi(\alpha + \beta)\]
となります。ここで、\( \psi(x) = \frac{d}{dx}\ln\Gamma(x) \) はディガンマ関数です。さらに、両辺に \( B(\alpha, \beta) \) をかけてやると、
\[ \frac{\partial}{\partial \alpha} B(\alpha, \beta) = B(\alpha, \beta)\,\bigl[\psi(\alpha) – \psi(\alpha + \beta)\bigr] \]
3.5. 最終式
以上より、
\[ E[\ln X] = \frac{1}{B(\alpha, \beta)} \frac{\partial}{\partial \alpha} B(\alpha, \beta) = \frac{1}{B(\alpha, \beta)} \cdot B(\alpha, \beta)\,\bigl[\psi(\alpha) – \psi(\alpha + \beta)\bigr] = \psi(\alpha) – \psi(\alpha + \beta) \]
したがって
\[ \boxed{ E[\ln X] \;=\; \psi(\alpha) \;-\; \psi(\alpha + \beta) } \]