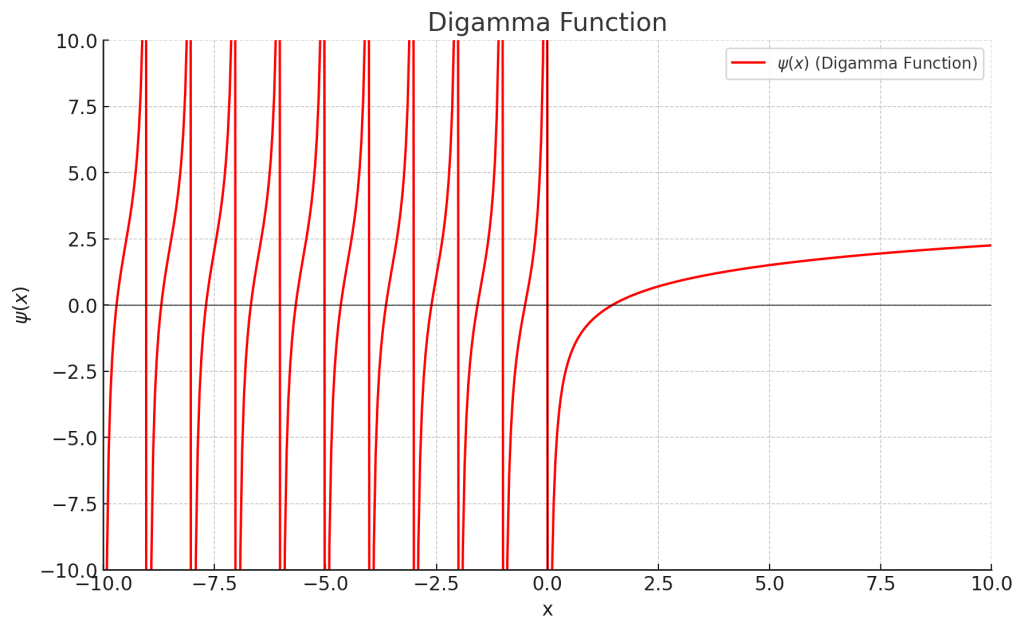
ディガンマ関数とは?定義と性質、Pythonによる数値計算について

「ディガンマ関数」という名前を聞いたことはありますか?数学や統計学に登場するこの関数は、ガンマ関数の対数微分として定義され、確率分布や特殊関数の解析に欠かせない重要な役割を果たします。
1. ディガンマ関数の定義
ディガンマ関数は、ガンマ関数 \( \Gamma(x) \) の対数の導関数として定義されます。
\[ \psi(x) = \frac{d}{dx} \log \Gamma(x) = \frac{\Gamma'(x)}{\Gamma(x)} \]
ここで、\( \Gamma(x) \) はガンマ関数を表します。
2. 性質
- 漸化式: \[ \psi(x+1) = \psi(x) + \frac{1}{x} \]
- z=1: \[ \psi(1) = -\gamma \] ここで、\( \gamma \) はオイラー=マスケローニ定数です。
- ベータ分布X:\[ E[\ln X] \;=\; \psi(\alpha) \;-\; \psi(\alpha + \beta)\]
2.1. ディガンマ関数の漸化式
ディガンマ関数 \(\psi(x)\) は、ガンマ関数 \(\Gamma(x)\) の対数微分として定義されます。
\[ \psi(x) = \frac{d}{dx} \log \Gamma(x) \]
ガンマ関数 \(\Gamma(x)\) は、次の性質を持ちます。
\[ \Gamma(x+1) = x \Gamma(x) \]
これを対数を取ることで次のようになります。
\[ \log \Gamma(x+1) = \log(x \Gamma(x)) = \log x + \log \Gamma(x) \]
この両辺を微分します。
\[ \frac{d}{dx} \log \Gamma(x+1) = \frac{d}{dx} (\log x + \log \Gamma(x)) \]
ここで、ディガンマ関数の定義により左辺は \(\psi(x+1)\) となり、右辺は次のようになります。
\[ \psi(x+1) = \frac{d}{dx} \log x + \frac{d}{dx} \log \Gamma(x) \]
\(\frac{d}{dx} \log x\) は \(\frac{1}{x}\) であり、\(\frac{d}{dx} \log \Gamma(x)\) は \(\psi(x)\) です。したがって、
\[ \psi(x+1) = \frac{1}{x} + \psi(x) \]
これにより、次の関係式が示されました。
\[ \psi(x+1) = \psi(x) + \frac{1}{x} \]
2.2. z=1のときのディガンマ関数
ガンマ関数の対数微分で得られる公式を利用して、ディガンマ関数 \(\psi(z)\) を導出します。
まず、ガンマ関数 \(\Gamma(z)\) の無限乗積表示から出発します。
\[ \frac{1}{\Gamma(z)} = \lim_{n \to \infty} \frac{n! \, n^z}{z(z+1)(z+2)\cdots(z+n)} \]
これの両辺の対数を取ると。
\[ \log \Gamma(z) = – \lim_{n \to \infty} \left( \sum_{k=0}^n \log(z + k) – z \log n – \log n! \right) \]
この式を \(z\) について微分すると、ディガンマ関数 \(\psi(z)\) を得ることができます。
\[ \psi(z) = \frac{d}{dz} \log \Gamma(z) = – \lim_{n \to \infty} \left( \sum_{k=0}^n \frac{1}{z + k} – \log n \right) \]
この公式に \(z = 1\) を代入すると、\(\psi(1)\) になります。
\[ \psi(1) = – \lim_{n \to \infty} \left( \sum_{k=0}^n \frac{1}{1 + k} – \log n \right) \]
\[ \psi(1) = – \lim_{n \to \infty} \left( \frac{1}{n+1} + \sum_{k=1}^n \frac{1}{k} – \log n \right) \]
\[ \psi(1) = – \left( \lim_{n \to \infty} \left( \frac{1}{n+1} \right) + \gamma \right) \]
$\displaystyle\lim_{n \to \infty} \frac{1}{n+1}$は \(0\) に収束するため、
\[ \psi(1) = – \gamma \]
\[ \gamma = \lim_{n \to \infty} \left( \sum_{k=1}^n \frac{1}{k} – \log n \right) \]
2.3. ベータ分布とディガンマ関数
Xがベータ分布に従うとき、
\[ E[\ln X] \;=\; \psi(\alpha) \;-\; \psi(\alpha + \beta)\]
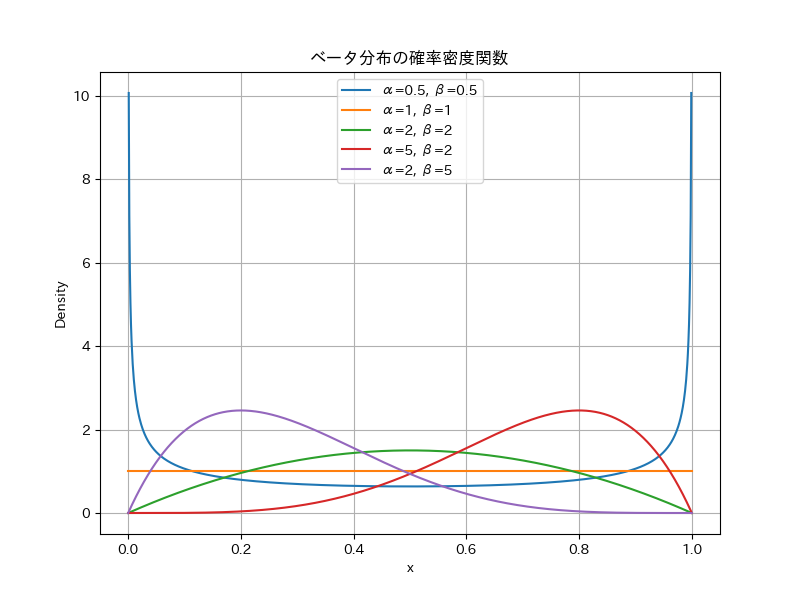
ベータ分布は、区間 \([0,1]\) 上で定義される確率分布です。
3. Pythonで数値計算
ディガンマ関数の値を数値的に計算するためのアルゴリズムは多くの数学ソフトウェアやライブラリに実装されています。例えば、PythonのSciPyライブラリでは scipy.special.digamma 関数が用意されています。
以下はPythonでディガンマ関数の値を計算する例です。
import scipy.special
# xの値
x = 5.0
# ディガンマ関数の値を計算
result = scipy.special.digamma(x)
print(result)
このように、ディガンマ関数は数学とその応用分野において広く利用される重要な関数です。