近接写像の意味、微分と計算例について

1. 近接写像とは？

近接写像（Proximal Operator）はある微分ができない点を含む関数 $f(x)$ を小さくしつつ、基準点 $a$ から極端に離れない点を探す。数式で書くと

二乗距離 $\tfrac12\lVert x-a\rVert^2$ が「遠くへ行き過ぎない」罰則を与えています。argminで最小値を与えるxを求めます。

ふゅか

近接写像って聞いたことある？なんだか難しそうだけど…。

はるか

…うん。関数の最小値を探す。でも、遠くに行き過ぎないようにしてる。

ふゅか

なるほど…つまり、ある点 a からあんまり離れないようにしながら、関数をできるだけ小さくする感じ？

はるか

そう。それが、$f(x) + \tfrac{1}{2} \lVert x – a \rVert^2$ を最小にするってこと。

1.1. 別の記法

近接写像はいろいろな書き方をされますが、次のように書かれることもあります。

2.  $f(x)=\lambda|x|$ の近接写像

$f(x)=\lambda|x|$ の近接写像を求めてみましょう。

$$ \operatorname{prox}_{f}(a) =\arg\min_{x\in\mathbb R} \Bigl\{\; \lambda|x|+\frac12(x-a)^2 \Bigr\}. $$

絶対値の区間分け

$$ |x|= \begin{cases} \;\;x & (x>0)\\ 0 & (x=0)\\ -\,x & (x<0) \end{cases} $$

したがって目的関数 $g(x)=\lambda|x|+\dfrac12(x-a)^2$ を 3 区間で分ける。

2.1. (i) $x>0$ の場合

$$ g(x)=\lambda x+\frac12(x-a)^2. $$

微分して 0 に置くと

$$ \lambda+(x-a)=0 \quad\Longrightarrow\quad x=a-\lambda. $$

この解が区間条件 $x>0$ を満たす ↔ $a>\lambda$。

2.2. (ii) $x<0$ の場合

$$ g(x)=\lambda(-x)+\frac12(x-a)^2 =-\,\lambda x+\frac12(x-a)^2. $$

微分して 0 に置くと

$$ -\lambda+(x-a)=0 \quad\Longrightarrow\quad x=a+\lambda. $$

区間条件 $x<0$ を満たす ↔ $a<-\lambda$。

2.3. (iii) $x=0$ 劣微分

関数 $f(x) = |x|$ は、点 $x = 0$ において微分可能ではない。したがって通常の勾配（導関数）を用いることができないため、代わりに劣勾配（subgradient）と呼ばれる概念を用いる。

ふゅか

$x=0$ のときは普通に微分できないから、劣微分ってのを使うんだよね？

はるか

うん。$|x|$ は0で折れてるから、普通の導関数ない。だから、傾きの範囲を使う。

劣勾配は凸関数に対して「その点での接線の傾きの全ての値の集合」を指し、記号 $\partial f(x)$ で表される。

この集合は一般には複数の値を含むため、最適性条件を記述する際に等号「=」ではなく、集合への所属を表す記号「$\in$」を用いる。

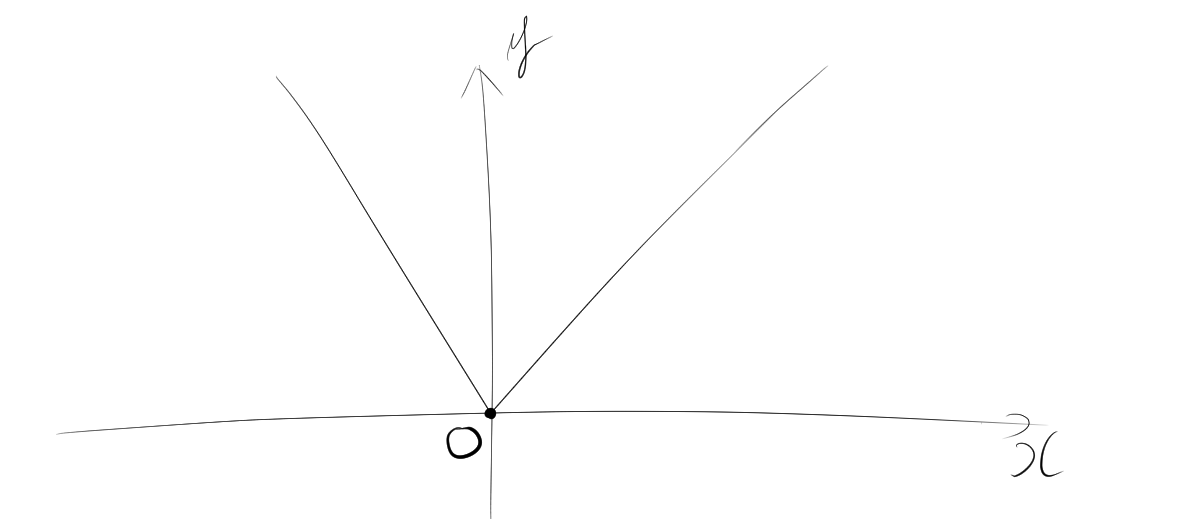
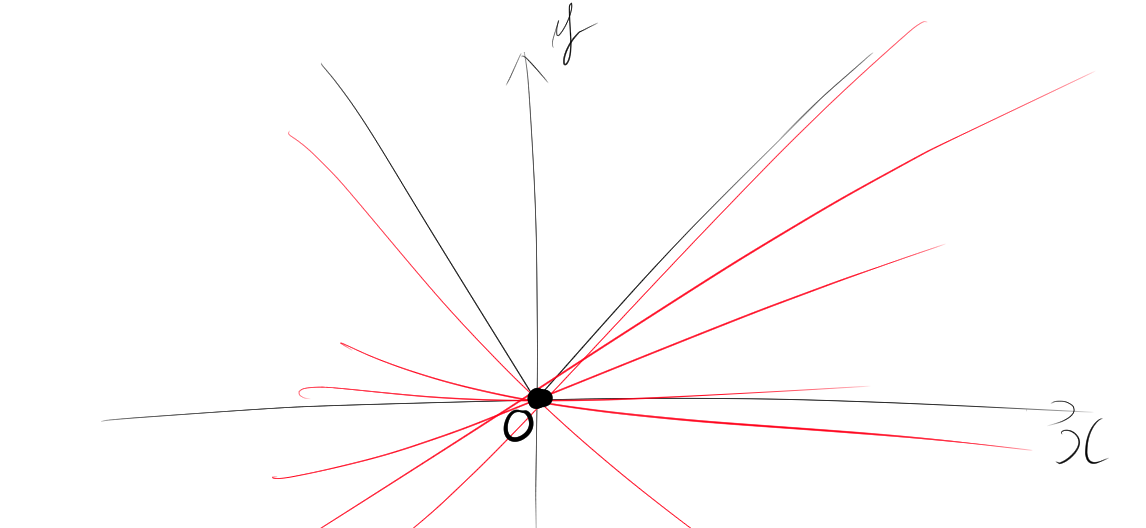
例えば、次のようなy=|x|の関数を考えたとする。その場合、$x=0$の点で微分ができない。

であるので、x=0の点では$[-1,1]$の範囲の傾きでいくらでも接線がとることができる。

では、今回の近接写像$\lambda|x|$の例を考えてみよう。

$$ \mathrm{prox}_f(a) = \arg\min_x \left\{ \lambda|x| + \frac{1}{2}(x – a)^2 \right\} $$

は以下のように記述される：

$$0 \in \lambda\,\partial|x| + (x – a)$$

ここで、特に $x = 0$ のとき $\partial |x| = [-1,1]$ であるため、

$$a\in[-\lambda,\lambda]$$

つまり、絶対値を使って

$$|a|\leq \lambda$$

結果をまとめると、

$$ \boxed{% \operatorname{prox}_f(a)= \begin{cases} a – \lambda & \text{if } a > \lambda \\[6pt] 0 & \text{if } |a| \le \lambda \\[6pt] a + \lambda & \text{if } a < -\lambda \end{cases}} $$

ここで注意したいことは、近接写像で求めるのはxであるということですね。

また、コンパクトな書き方をすると、

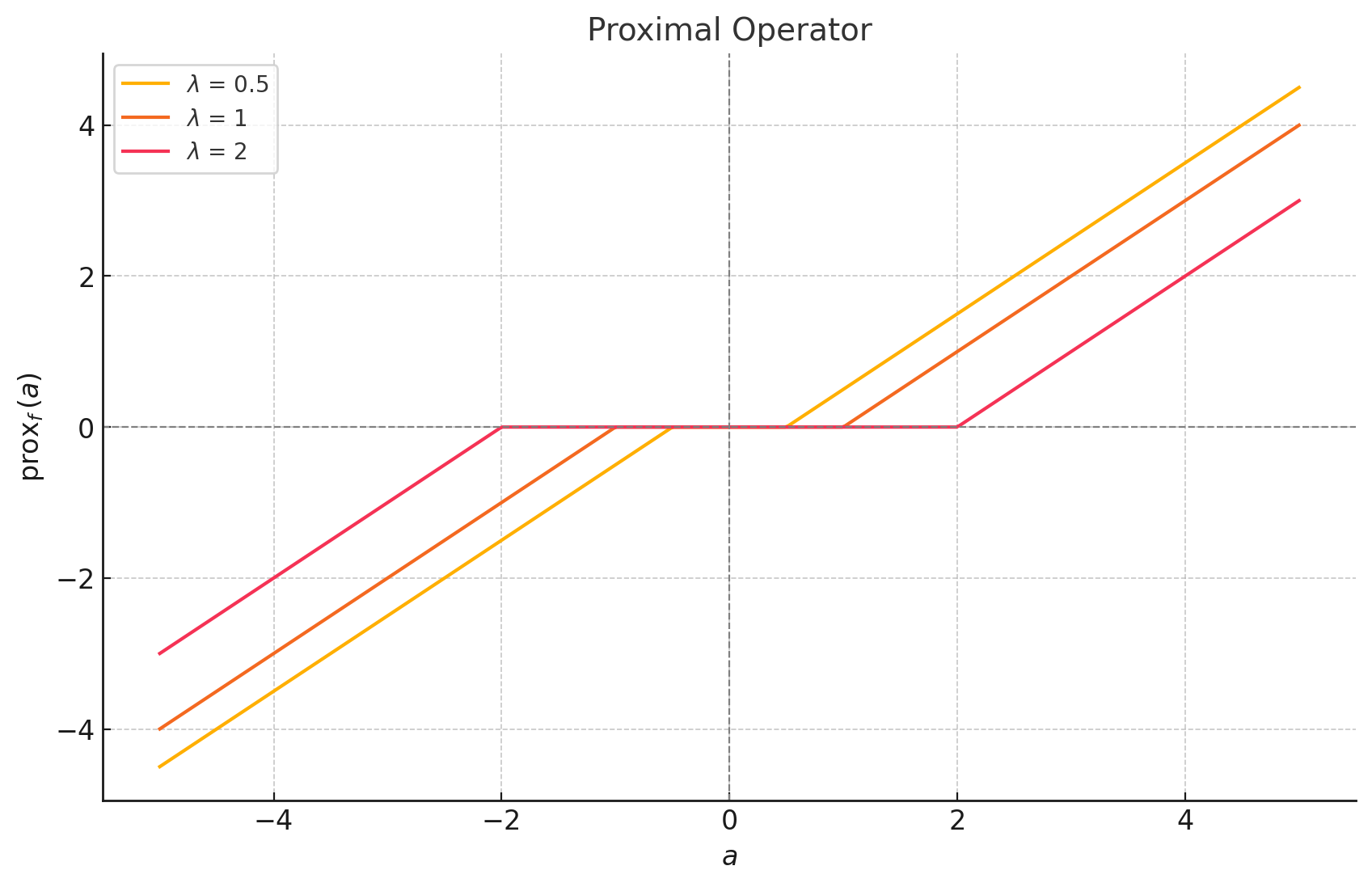
$$ \operatorname{prox}_f(a) =\operatorname{sign}(a)\; \max\!\left(|a|-\lambda,\;0\right) $$

とのように書くことができます。

今回の関数をプロットすると次のようになります。

3. コンパクトな書き方の意味

各項の意味を見ていきます。

3.1. $\operatorname{sign}(a)$

これは「符号関数（sign関数）」で、$a$ の符号だけを抽出します：

$$ \operatorname{sign}(a) = \begin{cases} +1 & \text{if } a > 0 \\ 0 & \text{if } a = 0 \\ -1 & \text{if } a < 0 \end{cases} $$

3.2. $\max(|a| – \lambda,\; 0)$

$a$ の絶対値から $\lambda$ を引いた値を計算

それが負になるときは 0 を採用 →「$\lambda$ 未満の小さい値は0に切り落とす（しきい値処理）」という意味になります。

3.3. 実際に成り立つか確認

$$ \operatorname{prox}_f(a) = \operatorname{sign}(a)\; \max\left(|a| – \lambda,\; 0\right) $$

この式が、場合分けした次の形と一致することを確かめます：

$$ \operatorname{prox}_f(a) = \begin{cases} a – \lambda & \text{if } a > \lambda \\[4pt] 0 & \text{if } |a| \le \lambda \\[4pt] a + \lambda & \text{if } a < -\lambda \end{cases} $$

3.3.1. ケース①：$\boldsymbol{a > \lambda}$

• $|a| = a$
• $|a| – \lambda = a – \lambda > 0$
• $\max(|a| – \lambda, 0) = a – \lambda$
• $\operatorname{sign}(a) = 1$

$$ \Rightarrow \operatorname{prox}_f(a) = 1 \cdot (a – \lambda) = a – \lambda $$

✅ 一致！

3.3.2. ケース②：$\boldsymbol{|a| \le \lambda}$（つまり $-\lambda \le a \le \lambda$）

• $|a| – \lambda \le 0$
• $\max(|a| – \lambda, 0) = 0$
• $\operatorname{sign}(a)$ は何であっても 0 倍されるので

$$ \Rightarrow \operatorname{prox}_f(a) = \operatorname{sign}(a) \cdot 0 = 0 $$

✅ 一致！

3.3.3. ケース③：$\boldsymbol{a < -\lambda}$

• $|a| = -a$
• $|a| – \lambda = -a – \lambda > 0$
• $\max(|a| – \lambda, 0) = -a – \lambda$
• $\operatorname{sign}(a) = -1$

$$ \Rightarrow \operatorname{prox}_f(a) = (-1) \cdot (-a – \lambda) = a + \lambda $$

✅ 一致！

→ よって、1行式は、3通りのケースすべてにおいて正しいといえます。