円の方程式の定義・一般形・性質・媒介変数表示について

1. 円の方程式
$$\large\left( x-a\right) ^{2}+\left( y-b\right) ^{2}=r^{2}$$
1.1. 円の方程式の導出
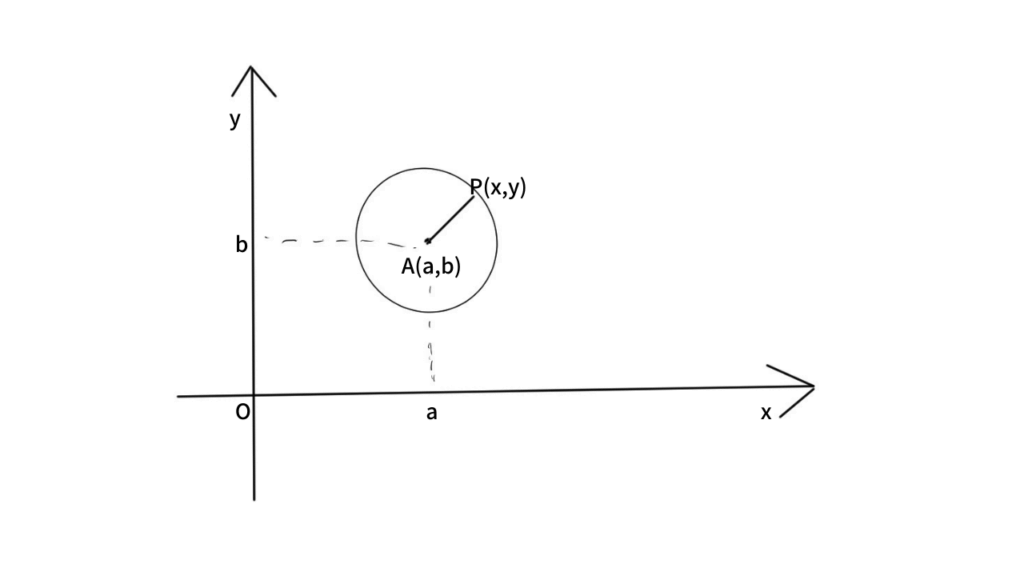
点 \( P(x, y) \) と、円の中心 \( A(a, b) \) の距離が半径 \( r \) であるとします。このとき、点 \( P \) は円の周上にあるため、次の関係が成り立ちます。
\[ PA = r \]
これは、点 \( P \) と中心 \( A \) の距離が常に \( r \) であることを意味します。ここで、点 \( P \) と \( A \) の間の距離は次のように表せます。
\[ PA^2 = r^2 \]
つまり、
\[ (x – a)^2 + (y – b)^2 = r^2 \]
この式は、点 \( P(x, y) \) が中心 \( A(a, b) \)、半径 \( r \) の円の方程式です。
このようにして、円の方程式が導出されました。
2. 円の方程式の一般形
$$x^2+y^2+lx+my+n=0$$
条件は次のようになります。
$$\dfrac{l^2+m^2-4n}{4}>0$$
2.1. 一般形の導出
\( (a, b) \) は円の中心、\( r \) は半径の円の方程式は次のようになります。
\[ (x – a)^2 + (y – b)^2 = r^2 \]
円の方程式を展開すると、
\[ (x^2 – 2ax + a^2) + (y^2 – 2by + b^2) = r^2 \]
\[ x^2 + y^2 – 2ax – 2by + a^2 + b^2 = r^2 \]
\[ x^2 + y^2 – 2ax – 2by + (a^2 + b^2 – r^2) = 0 \]
ここで、一般形 \[ x^2 + y^2 + lx + my + n = 0 \] に対応させるために、次のように置き換える。
- \( l = -2a \)
- \( m = -2b \)
- \( n = a^2 + b^2 – r^2 \)
このことから、一般形を導出できる。
2.2. 条件の導出
$x,y$に関して平方完成を行うと、
$\left(x+\dfrac{l}{2}\right)^{2}-\dfrac{l^2}{4}+\left(y+\dfrac{m}{2}\right)^{2}-\dfrac{m^2}{4}+n=0$
$\therefore\left(x+\dfrac{l}{2}\right)^{2}+\left(y+\dfrac{m}{2}\right)^{2}=\dfrac{l^2+m^2-4n}{4}$
となり、左辺は二乗の和だから、
$\left(x+\dfrac{l}{2}\right)^{2}+\left(x+\dfrac{m}{2}\right)^{2}>0$
左辺が正であるため、右辺も正であることがわかる。したがって、
$\dfrac{l^2+m^2-4n}{4}>0$
2.3. 条件の場合分け
$\dfrac{l^2+m^2-4n}{4}>0$のとき、
中心$(-\dfrac{l}{2},-\dfrac{m}{2})$、半径$\dfrac{\sqrt{l^{2}+m^{2}-4n}}{2}$の円を表す。
$\dfrac{l^2+m^2-4n}{4}=0$のとき、
$(-\dfrac{l}{2},-\dfrac{m}{2})$の点を表す。
$\dfrac{l^2+m^2-4n}{4}<0$のとき、
表す図形はなし。
3. 円の方程式の性質
3.1. 媒介変数表示
$$x=r\cos \theta +a$$
$$y=r\sin \theta +b$$
媒介変数表示された \( x \) と \( y \) を、距離 \( PA^2 \) に代入すると、次のようになります。
\[ PA^2 = \left( r\cos \theta + a – a \right)^2 + \left( r\sin \theta + b – b \right)^2 \]
まず、\( a \) と \( b \) が消えるため、次のように簡単化できます。
\[ PA^2 = r^2\cos^2 \theta + r^2\sin^2 \theta \]
さらに、三角関数の関係式 \( \cos^2 \theta + \sin^2 \theta = 1 \) を用いると、
\[ PA^2 = r^2 \left( \cos^2 \theta + \sin^2 \theta \right) = r^2 \]
3.2. 単位円
特に、中心が原点 \( (a = 0, b = 0) \) で、半径が 1 (\( r = 1 \)) の場合、この円は単位円と呼ばれます。単位円の方程式は次のように表せます。
\[ x^2 + y^2 = 1 \]
また、単位円において、媒介変数表示は次のように記述できます。
\[ x = \cos \theta, \quad y = \sin \theta \]





