ペル方程式の解き方、極限√dへの収束について

1. ペル方程式

2. 解の見つけ方

ペル方程式では以下のステップを行うことでx,yの解を見つけることができる。

2.1. ステップ1

最小の正の解$x_{1}$、$y_{1}$を見つける。

2.2. ステップ2

$\alpha=x_{1}+y_{1}\sqrt{d}$と置いて、$\alpha$をk乗する。

$$\alpha^k=x_{k}+y_{k}\sqrt{d}$$

ここで現れる $x_k$ と $y_k$ は、$k$ 番目のペル方程式 $x^2 – dy^2 = 1$ の解になります。つまり、$\alpha$ を何度も累乗していくことで、新しい解 $(x_k, y_k)$ が次々と得られるというわけです。

この方法を繰り返していけば、初めの基本解 $(x_1, y_1)$ から、すべての正の整数解を順番に求めることができます。基本解から出発して、$\alpha^2, \alpha^3, \alpha^4,\dots$ と計算していけば、それぞれに対応する $(x_2, y_2), (x_3, y_3), (x_4, y_4), \dots$ が次々と現れます。

3. 漸化式で考える

$\alpha^k=x_{k}+y_{k}\sqrt{d}$であることから$\alpha^{k+1}$を考えると、

$$\begin{align*} x_{k+1}+y_{k+1}\sqrt{d} &= \alpha^{k+1} \\ &= \alpha^{k}\alpha \\ &= (x_{k}+y_{k}\sqrt{d})(x_{1}+y_{1}\sqrt{d}) \\ &= (x_{k}x_{1}+y_{k}y_{1}d)+(x_{k}y_{1}+y_{k}x_{1})\sqrt{d} \end{align*}$$

したがって、恒等式であることから、以下のような連立漸化式を作ることができる。

$$\begin{cases} x_{k+1} = x_k x_1 + y_k y_1 d \\ y_{k+1} = x_k y_1 + y_k x_1 \end{cases} $$

4. 解を求める例

ペル方程式の解を求めてみましょう。

正の最小解は$x_{1}=1$、$y_{1}=1$であるため、$\alpha=x_{1}+y_{1}\sqrt{2}$と置く。$x_{4}$、$y_{4}$まで求める。

$\alpha$を2乗すると、

$$\alpha^2=(1+\sqrt{2})^2=1+2\sqrt{2}+2=3+2\sqrt{2}$$

したがって、$x_{2}=3$、$y_{2}=2$となる。$\alpha$を3乗すると、$\alpha^2$と$\alpha$の積であると考えて、

$$\alpha^3=(1+\sqrt{2})^3=(3+2\sqrt{2})(1+\sqrt{2})=7+5\sqrt{2}$$

したがって、$x_{3}=7$、$y_{3}=5$となる。

$\alpha$を4乗すると、$\alpha^2$の2乗であると考えて、

$$\alpha^4=(1+\sqrt{2})^4=(3+2\sqrt{2})^2=17+12\sqrt{2}$$

したがって、$x_{4}=17$、$y_{4}=12$となる。

このように解を求めることができます。

4.1. $\sqrt{2}の近似$

上記で求めた解の$\frac{x}{y}$は、$\sqrt{2}=1.414・・・$の近似になります。

$$\begin{align*} \frac{x_1}{y_1} &= 1 \\ \frac{x_2}{y_2} &= 1.5 \\ \frac{x_3}{y_3} &= 1.4 \\ \frac{x_4}{y_4} &= 1.41666\ldots \end{align*} $$

だんだんと$\sqrt{2}=1.414・・・$に近づきます。その理由は、ペル方程式を式変形するとわかります。ペル方程式の両辺を$y^2$で割ると、

$$\displaystyle\left(\frac{x}{y}\right)^2-2=\displaystyle\left(\frac{1}{y}\right)^2$$

となります。つまり、$y$の値が大きくなればなるほど右辺の$\displaystyle\left(\frac{1}{y}\right)^2$は0に近づきます。よって、左辺の$\displaystyle\left(\frac{x}{y}\right)^2$は2に近づくため、$\frac{x}{y}$は$\sqrt{2}$に近づく。

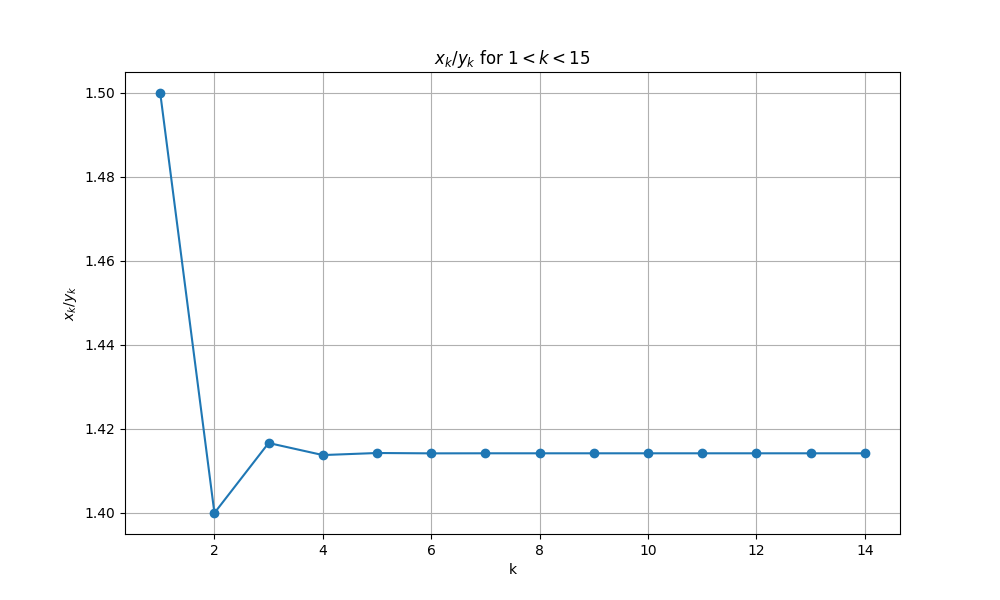
4.2. グラフでプロットする

$1\leq k \leq 15$の範囲で$\frac{x}{y}$をグラフにしてプロットしてみます。

4.3. 極限で確かめる

$$x_{k+1}=x_{k}x_{1}+y_{k}y_{1}d$$

$$y_{k+1}=x_{k}y_{1}+y_{k}x_{1}$$

であることから、

$$x_{k+1}=x_{k}+2y_{k}$$

$$y_{k+1}=x_{k}+y_{k}$$

ここで、$\left|\displaystyle\frac{x_{n+1}}{y_{n+1}}-\sqrt{2}\right|$　について考える。

\[ \begin{aligned} \left| \frac{x_{n+1}}{y_{n+1}} – \sqrt{2} \right| &= \left| \frac{x_{n} + 2y_{n}}{x_{n} + y_{n}} – \sqrt{2} \cdot \frac{x_{n} + y_{n}}{x_{n} + y_{n}} \right| \\ &= \left| \frac{(1 – \sqrt{2}) x_{n} – \sqrt{2} (1 – \sqrt{2}) y_{n}}{x_{n} + y_{n}} \right| \\ &= (\sqrt{2} – 1) \left| \frac{x_{n} – \sqrt{2} y_{n}}{x_{n} + y_{n}} \right| \end{aligned} \]

$y_{n+1}=x_{n}+y_{n}$であることから、

$$\begin{align*} &= (\sqrt{2}-1) \left|\frac{x_{n}-\sqrt{2}y_{n}}{y_{n+1}}\right| \\ &= (\sqrt{2}-1) \left| y_{n} \frac{\frac{x_{n}}{y_{n}}-\sqrt{2}}{y_{n+1}} \right| \\ &< (\sqrt{2}-1) \left| \frac{x_{n}}{y_{n}} – \sqrt{2} \right| \end{align*}$$

ここで、$y_{n+1}=x_{n}+y_{n}>y_{n}$より、$\displaystyle\frac{y_{n}}{y_{n+1}}<1$であることから不等式が求められる。また、$\sqrt{2}-1$は$0<\sqrt{2}-1<1$である。

$$\begin{align*} \left|\frac{x_{n}}{y_{n}}-\sqrt{2}\right| &< (\sqrt{2}-1)\left|\frac{x_{n-1}}{y_{n-1}}-\sqrt{2}\right| \\ &< (\sqrt{2}-1)^2\left|\frac{x_{n-2}}{y_{n-2}}-\sqrt{2}\right| \\ &< (\sqrt{2}-1)^{n-1}\left|\frac{x_{1}}{y_{1}}-\sqrt{2}\right| \\ &< (\sqrt{2}-1)^{n-1} \left|1-\sqrt{2}\right| \\ &< (\sqrt{2}-1)^{n} \end{align*}$$

不等式を作ると、

$$0<\displaystyle\lim_{n\rightarrow\infty}\left|\displaystyle\frac{x_{n}}{y_{n}}-\sqrt{2}\right|<\lim_{n\rightarrow\infty}(\sqrt{2}-1)\left|\displaystyle\frac{x_{n-1}}{y_{n-1}}-\sqrt{2}\right|$$

$$0<\displaystyle\lim_{n\rightarrow\infty}\left|\displaystyle\frac{x_{n}}{y_{n}}-\sqrt{2}\right|<\displaystyle\lim_{n\rightarrow\infty}\left|(\sqrt{2}-1)^{n}\right|$$

$\displaystyle\lim_{n\rightarrow\infty}\left|(\sqrt{2}-1)^{n}\right|=0$である。

はさみうちの原理より、$\displaystyle\lim_{n\rightarrow\infty}\left|\displaystyle\frac{x_{n}}{y_{n}}-\sqrt{2}\right|=0$

したがって、$\displaystyle\lim_{n\rightarrow\infty}\displaystyle\frac{x_{n}}{y_{n}}=\sqrt{2}$