【面積比】重心が三角形の面積を1:1:1に分けることの証明について
1. 重心とは
まず、重心について復習しましょう。三角形の重心は、3本の中線が交わる一点です。中線とは、三角形の各頂点からその対辺の中点に引かれた線のことです。この3本の中線は必ず一点で交わり、その交点が重心となります。
2. 重心が面積をどう分けるのか？
重心と頂点ABCで作る三角形は、三角形ABCを3つに分割します。このとき、以下の特徴があります。
3. なぜ面積比が1:1:1になるのか？
3.1. 図形の性質を利用した証明
三角形ABCの面積をS、重心をGとする。また、線分 \( AG \) を延長して、辺 \( BC \) と交わる点を \( D \) とします。
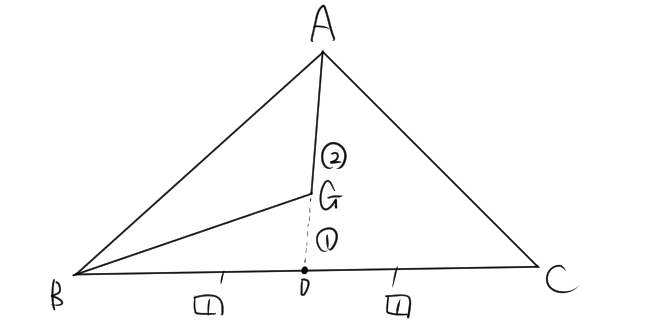三角形 \( ABD \) の面積は点 \( D \) が辺 \( BC \) の中点であることから
$$S_{\text{三角形ABD}}=\frac{1}{2}S$$
次に、線分 \( AD \) を重心 \( G \) が \( 2:1 \) に内分しているため、三角形 \( ABG \) の面積は三角形 \( ABD \) の面積の \( \frac{2}{3} \) となります。
$$\begin{align*} S_{\text{三角形ABG}} &= \frac{2}{3}S_{\text{三角形ABD}} \\ &= \frac{2}{3} \times \frac{1}{2}S \\ &= \frac{1}{3}S \end{align*}$$
同様に、三角形 \( ACG \) 、三角形 \( BCG \) の面積も同じように計算でき、三角形の面積比が次のように求まります。
\[ S_{\text{三角形ACG}} : S_{\text{三角形BCG}} : S_{\text{三角形ABG}} =\frac{1}{3}S: \frac{1}{3}S :\frac{1}{3}S = 1:1:1\]
3.2. 座標を利用した証明
重心 \( G \) を原点とする三角形を考えます。
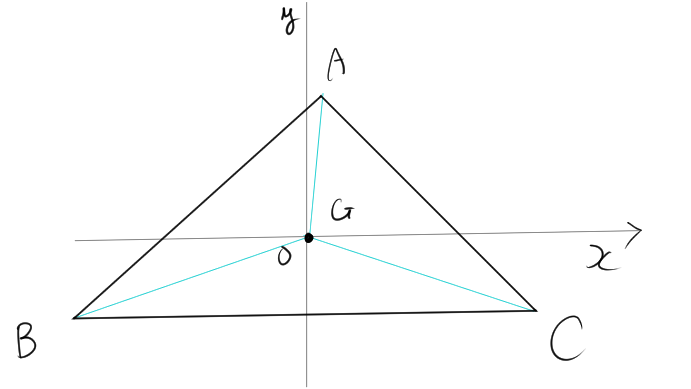この三角形の頂点を \( A(a_x, a_y) \), \( B(b_x, b_y) \), \( C(c_x, c_y) \) とします。重心 \( G \) が原点にあるため、重心の座標を \((0, 0)\) として計算を進めます。サラスの公式より、三角形 \( ABG \) と三角形 \( ACG \) の面積は
$$S_{\text{三角形ABG}}=\frac{1}{2}|a_xb_y-a_yb_x|$$
$$S_{\text{三角形ACG}}=\frac{1}{2}|a_xc_y-a_yc_x|$$
重心の座標は$(\frac{a_x+b_x+c_x}{3},\frac{a_y+b_y+c_y}{3})$であり、原点であることから
$$\left(\frac{a_x+b_x+c_x}{3},\frac{a_y+b_y+c_y}{3}\right)=(0,0)$$
この式から、頂点 \( B \) の座標 \( b_x \)、\( b_y \) を次のように求めることができます。
$$ b_x = -a_x - c_x, \quad b_y = -a_y - c_y $$
ここで、三三角形 \( ABG \) の面積式にこの \( b_x \)、\( b_y \) の値を代入して、計算すると
\[ \begin{align*} S_{\text{三角形ABG}} &= \frac{1}{2} |a_x(-a_y - c_y) - a_y(-a_x - c_x)| \\ &= \frac{1}{2} | -a_x a_y - a_x c_y + a_y a_x + a_y c_x | \\ &= \frac{1}{2} | -a_x c_y + a_y c_x | \\ &= \frac{1}{2} | a_x c_y - a_y c_x | \\ &=S_{\text{三角形ACG}} \end{align*} \]
三角形 \( ABG \) の面積と \( ACG \) の面積が等しいことがわかります。これを同様に計算してくことで、
$$S_{\text{三角形AGC}}=S_{\text{三角形ACG}} =S_{\text{三角形ABG}}$$
したがって、三角形 \( ABG \)、\( ACG \)、\( AGC \) の面積比は次のようになります。
\[ S_{\text{三角形AGC}} : S_{\text{三角形ACG}} : S_{\text{三角形ABG}} =1:1:1\]
