マスジョイ
PR
C言語 GO Haskell Java javascript Octave PHP python3 R 確率・統計
更新:2025/02/27

様々なプログラミング言語による最小二乗法の導出（Python、Java、C、GO、Javascript、R、Haskell、Java）

目次

1. 最小二乗法

最小二乗法（Least Squares Method）は、与えられたデータに対して最適な近似曲線を求める手法の一つです。これは、データ点と近似曲線の誤差の二乗和を最小化することを目的としています。

最小二乗法を使って、データ点 \((x_i, y_i)\) に対する直線 \[ y = ax + b \] を求めるための公式は次の通りです。

1.1. 傾き \( a \) の計算

\[ a = \frac{n \sum{x_i y_i} – \sum{x_i} \sum{y_i}}{n \sum{x_i^2} – (\sum{x_i})^2} \]

1.2. 切片 \( b \) の計算

\[ b = \frac{\sum{y_i} – a \sum{x_i}}{n} \]

1.3. 式の意味

  • \( n \) はデータ点の個数
  • \( x_i, y_i \) は各データ点の値
  • \( \sum{x_i} \) は \( x \) の総和
  • \( \sum{y_i} \) は \( y \) の総和
  • \( \sum{x_i y_i} \) は \( x \) と \( y \) の積の総和
  • \( \sum{x_i^2} \) は \( x \) の二乗の総和

1.4. 計算手順

  1. データ点が \( n \) 個あるとする
  2. \( x \) の総和 \( \sum{x_i} \)、\( y \) の総和 \( \sum{y_i} \) を求める
  3. \( x \) の二乗の総和 \( \sum{x_i^2} \) を求める
  4. \( x \) と \( y \) の積の総和 \( \sum{x_i y_i} \) を求める
  5. 上記の公式を使って \( a \)（傾き）と \( b \)（切片）を求める

1.5. 具体例

例えば、データ点 \( (1,2), (2,3), (3,5), (4,7), (5,11) \) を使って計算すると：

\[ \sum{x_i} = 1+2+3+4+5 = 15 \]

\[ \sum{y_i} = 2+3+5+7+11 = 28 \]

\[ \sum{x_i^2} = 1^2 + 2^2 + 3^2 + 4^2 + 5^2 = 55 \]

\[ \sum{x_i y_i} = (1 \times 2) + (2 \times 3) + (3 \times 5) + (4 \times 7) + (5 \times 11) = 106\]

\[ a = \frac{5 \times 106- 15 \times 28}{5 \times 55 – 15^2} = \frac{530- 420}{275 – 225} = \frac{110}{50} = 2.2\]

\[ b = \frac{28 – 2.2 \times 15}{5} = \frac{28 -33}{5} = \frac{-5}{5} = -1 \]

したがって、回帰直線の式は： \[ y = 2.2x -1  \]

この公式を各言語で実装して、データに最適な回帰直線を求めてみましょう！

2. 実装

2.1. Python

Pythonでは、NumPyを使うと簡単に最小二乗法を実装できます。

import numpy as np

# サンプルデータ (x, y)
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 3, 5, 7, 11])

# 最小二乗法 (線形回帰)
A = np.vstack([x, np.ones(len(x))]).T
a, b = np.linalg.lstsq(A, y, rcond=None)[0]

print(f"傾き: {a}, 切片: {b}")

NumPyの np.linalg.lstsq() を使うと、係数 a と切片 b を簡単に求めることができます。

2.2. C言語

C言語では、次のように計算を行います。

#include <stdio.h>

int main() {
    double x[] = {1, 2, 3, 4, 5};
    double y[] = {2, 3, 5, 7, 11};
    int n = 5;

    double sum_x = 0, sum_y = 0, sum_x2 = 0, sum_xy = 0;

    for (int i = 0; i < n; i++) {
        sum_x += x[i];
        sum_y += y[i];
        sum_x2 += x[i] * x[i];
        sum_xy += x[i] * y[i];
    }

    double a = (n * sum_xy - sum_x * sum_y) / (n * sum_x2 - sum_x * sum_x);
    double b = (sum_y - a * sum_x) / n;

    printf("傾き: %lf, 切片: %lf\n", a, b);
    return 0;
}

手動でΣ（シグマ）計算を行い、最小二乗法の公式を適用しています。

2.3. JavaScript

JavaScriptでは、ブラウザのコンソールやNode.jsで実行できます。

function leastSquares(x, y) {
    let n = x.length;
    let sum_x = 0, sum_y = 0, sum_x2 = 0, sum_xy = 0;

    for (let i = 0; i < n; i++) {
        sum_x += x[i];
        sum_y += y[i];
        sum_x2 += x[i] * x[i];
        sum_xy += x[i] * y[i];
    }

    let a = (n * sum_xy - sum_x * sum_y) / (n * sum_x2 - sum_x * sum_x);
    let b = (sum_y - a * sum_x) / n;

    return { a, b };
}

let x = [1, 2, 3, 4, 5];
let y = [2, 3, 5, 7, 11];

let result = leastSquares(x, y);
console.log(`傾き: ${result.a}, 切片: ${result.b}`);

この関数は配列 x と y を受け取り、最小二乗法で回帰直線の係数を求めます。

2.4.  R

Rは統計解析向けの言語なので、最小二乗法は非常に簡単に実装できます。

x <- c(1, 2, 3, 4, 5)
y <- c(2, 3, 5, 7, 11)

model <- lm(y ~ x)

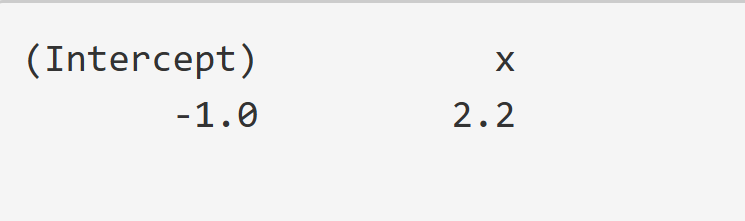
print(coef(model))  # 傾きと切片を出力

lm(y ~ x) を使うことで、線形回帰モデルを簡単に作成できます。

2.5. Octave

Octaveでは、行列演算を使って最小二乗法を求められます。

x = [1 2 3 4 5]';
y = [2 3 5 7 11]';

A = [x ones(length(x), 1)];
coeff = A \ y;

disp(['傾き: ', num2str(coeff(1)), ', 切片: ', num2str(coeff(2))]);

行列を使って直接計算することで、PythonのNumPyのように簡単に最小二乗法を求めることができます。

2.6. Java

Javaでは、標準ライブラリを使って手動で計算する方法が一般的です。

public class LeastSquares {
    public static void main(String[] args) {
        double[] x = {1, 2, 3, 4, 5};
        double[] y = {2, 3, 5, 7, 11};
        int n = x.length;

        double sum_x = 0, sum_y = 0, sum_x2 = 0, sum_xy = 0;

        for (int i = 0; i < n; i++) {
            sum_x += x[i];
            sum_y += y[i];
            sum_x2 += x[i] * x[i];
            sum_xy += x[i] * y[i];
        }

        double a = (n * sum_xy - sum_x * sum_y) / (n * sum_x2 - sum_x * sum_x);
        double b = (sum_y - a * sum_x) / n;

        System.out.println("傾き: " + a + ", 切片: " + b);
    }
}

2.7. PHP

<?php
function leastSquares($x, $y) {
$n = count($x);
$sum_x = 0;
$sum_y = 0;
$sum_x2 = 0;
$sum_xy = 0;

for ($i = 0; $i < $n; $i++) {
$sum_x += $x[$i];
$sum_y += $y[$i];
$sum_x2 += $x[$i] * $x[$i];
$sum_xy += $x[$i] * $y[$i];
}

// 最小二乗法の公式に基づく計算
$a = ($n * $sum_xy - $sum_x * $sum_y) / ($n * $sum_x2 - $sum_x * $sum_x);
$b = ($sum_y - $a * $sum_x) / $n;

return [$a, $b];
}

$x = [1, 2, 3, 4, 5];
$y = [2, 3, 5, 7, 11];

list($a, $b) = leastSquares($x, $y);

echo "傾き: $a, 切片: $b\n";
?>

2.8. Haskell

-- 最小二乗法の計算関数
leastSquares :: [Double] -> [Double] -> (Double, Double)
leastSquares x y =
    let n = fromIntegral (length x)
        sumX  = sum x
        sumY  = sum y
        sumX2 = sum (map (^2) x)
        sumXY = sum (zipWith (*) x y)
        a = (n * sumXY - sumX * sumY) / (n * sumX2 - sumX^2)
        b = (sumY - a * sumX) / n
    in (a, b)

main :: IO ()
main = do
    let x = [1, 2, 3, 4, 5]
        y = [2, 3, 5, 7, 11]
        (a, b) = leastSquares x y
    putStrLn $ "傾き: " ++ show a ++ ", 切片: " ++ show b

2.9. GO lang

package main

import (
	"fmt"
)

func leastSquares(x, y []float64) (float64, float64) {
	n := float64(len(x))
	var sumX, sumY, sumX2, sumXY float64

	for i := 0; i < len(x); i++ {
		sumX += x[i]
		sumY += y[i]
		sumX2 += x[i] * x[i]
		sumXY += x[i] * y[i]
	}

	// 最小二乗法の公式に基づく計算
	a := (n*sumXY - sumX*sumY) / (n*sumX2 - sumX*sumX)
	b := (sumY - a*sumX) / n

	return a, b
}

func main() {
	x := []float64{1, 2, 3, 4, 5}
	y := []float64{2, 3, 5, 7, 11}

	a, b := leastSquares(x, y)
	fmt.Printf("傾き: %f, 切片: %f\n", a, b)
}

ホームに戻る