複素数平面上の図形とベクトルの意味・例題について

1. 複素数のベクトル的な考え方

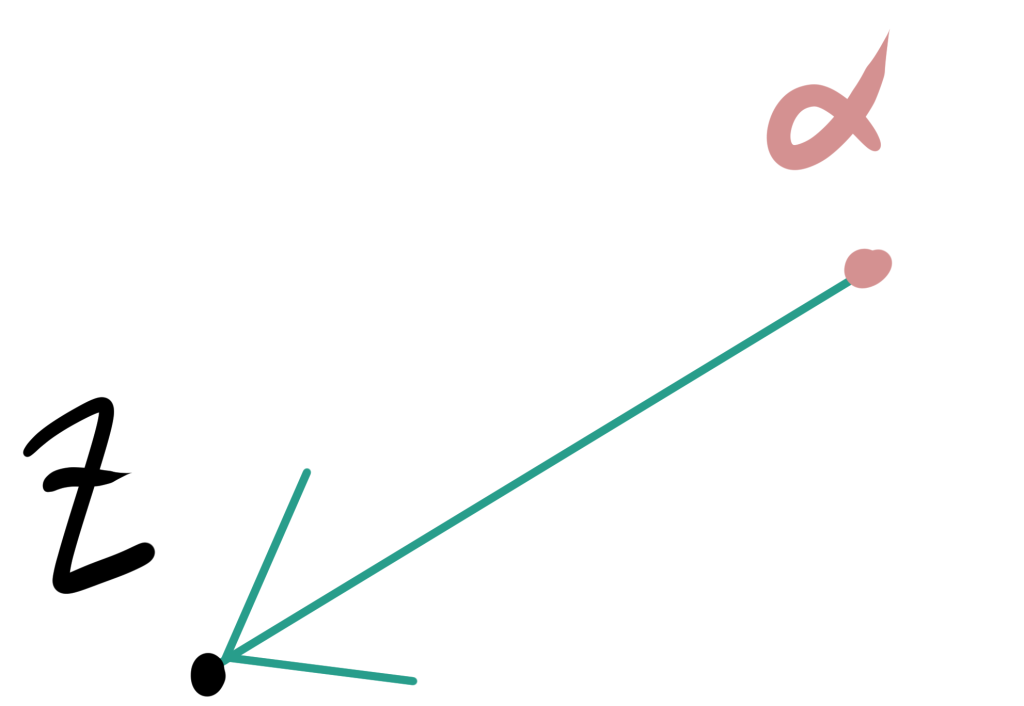
そのため、$|z-\alpha|$は$\alpha$から$z$までの距離を表します。

例えば、

$|z-\alpha|=r$

は$\alpha$から$z$までの距離がr(一定)になっているということを表します。

1.1. 図形的に考える例題

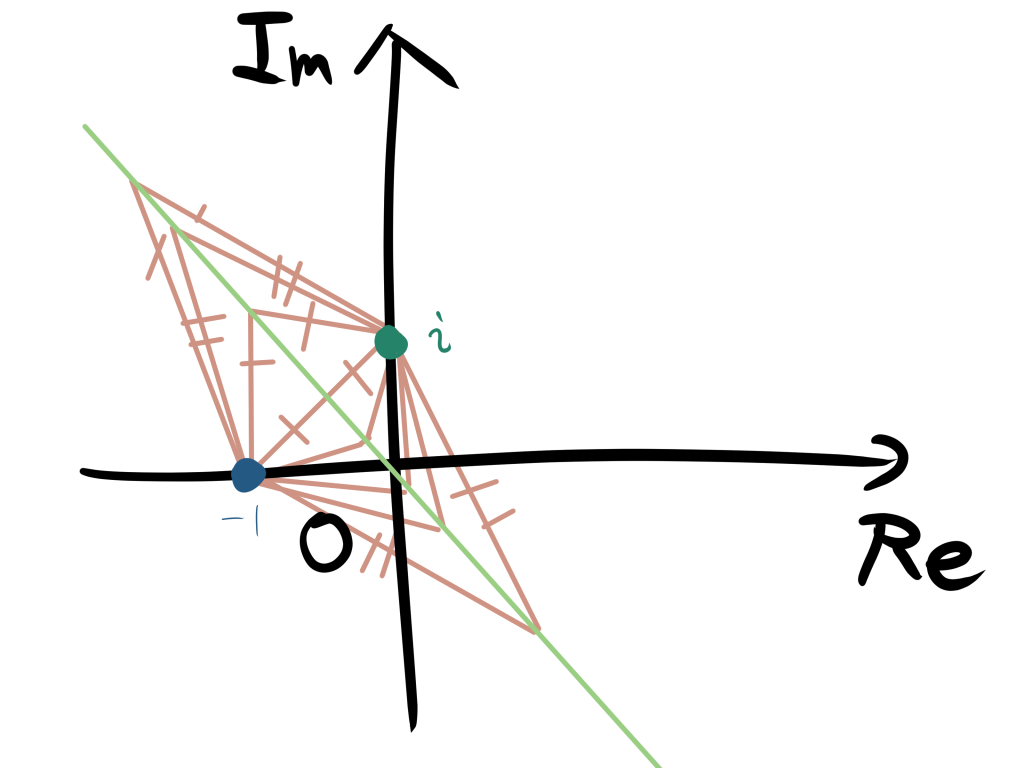
$(1)$ $-1$から$z$までの距離とiからzまでの距離が等しいという図形である。
距離が等しいというイメージは以下のようになります。

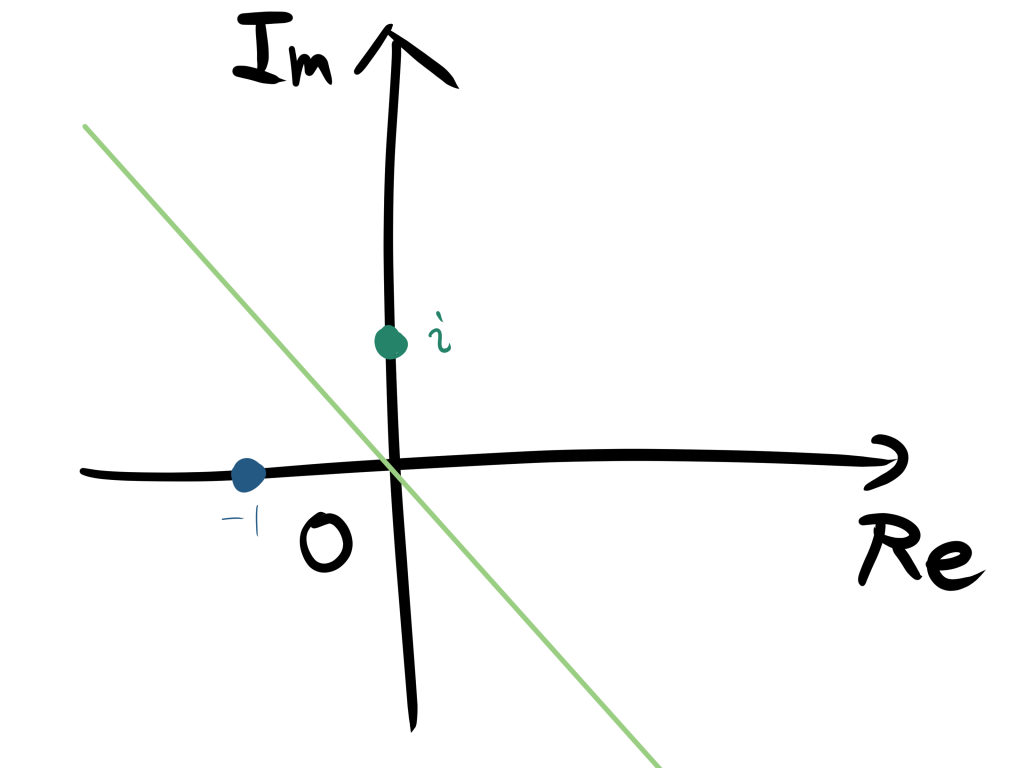
そのため、直線であることがわかるから以下のようになります。

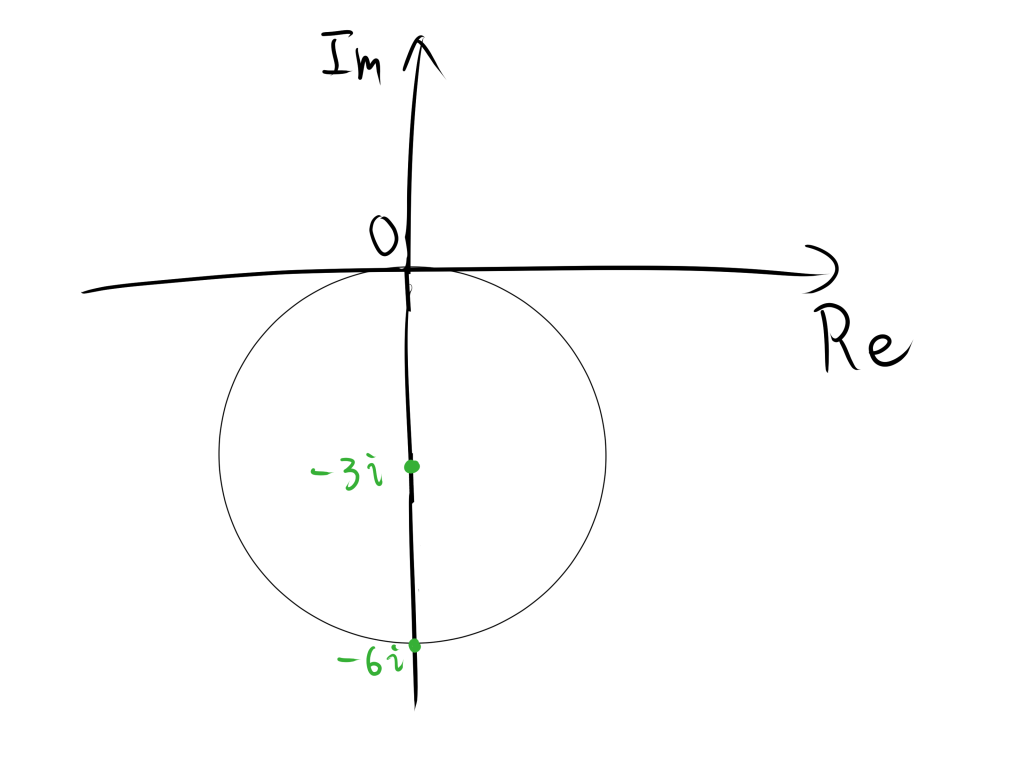
$(2)$　 $-3i$から$z$までの距離が$3$である図形である。
イメージは以下のようになります。

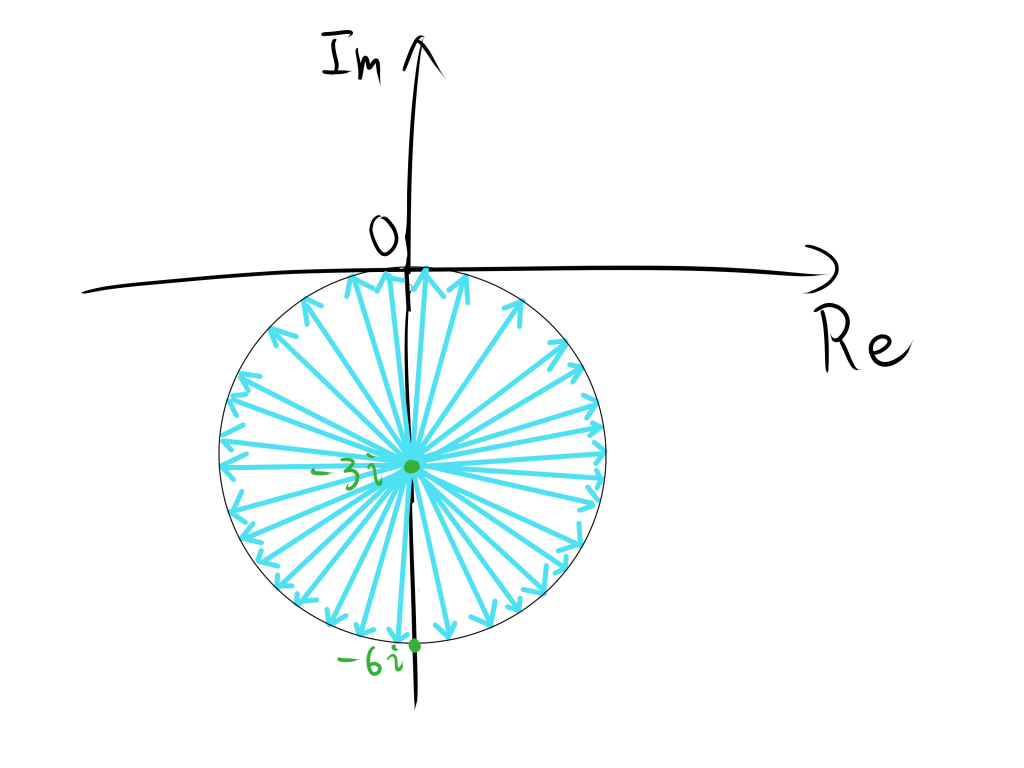
そのため、$-3i$を中心とする半径3の円であることがわかるから以下のようになります。

2. ベクトル的な考えができる理由

この疑問は計算的に考えると解決することができます。
ベクトルについてまず考えます。

$\vec{OA}=\begin{bmatrix} a_1 \\ a_2 \\ \end{bmatrix}$$\vec{OB}=\begin{bmatrix} b_1 \\ b_2 \\ \end{bmatrix}$とする。

$\vec{AB}=\vec{OB}-\vec{OA}$

$=\begin{bmatrix} b_1-a_1 \\ b_2-a_2 \\ \end{bmatrix}$

単位ベクトル$e_1=\begin{bmatrix} 1 \\ 0 \\ \end{bmatrix}$、$e_2=\begin{bmatrix} 0 \\ 1 \\ \end{bmatrix}$を用いて表すと、

$\vec{AB}=\begin{bmatrix} b_1-a_1 \\ b_2-a_2 \\ \end{bmatrix}$

$=(b_1-a_1)e_1+(b_2-a_2)e_2$

次に複素数について考えます。虚数単位を$i$とします。
複素数$a,b$を以下のようにあらわすとする。

$a=a_1+a_2i$

$b=b_1+b_2i$

このとき、$a_1,a_2,b_1,b_2$は実数である。

$b-a=(b_1-a_1)+(b_2-a_2)i$

ベクトルで似たような形の数式が出てきましたよね。では、ベクトルは成分表示されているので、複素数の成分表示を考えてみましょう。

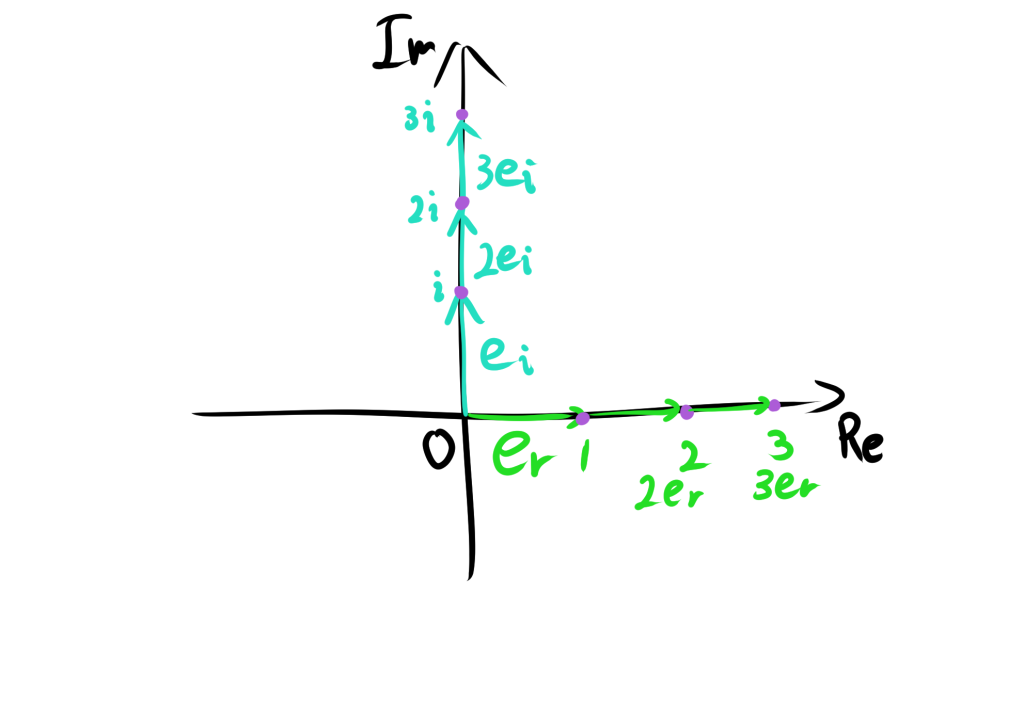
ここで、単位ベクトル$e_r=\begin{bmatrix} 1 \\ 0 \\ \end{bmatrix}$、$e_i=\begin{bmatrix} 0 \\ i \\ \end{bmatrix}$を用いて表すと、$b-a$の成分は以下のようにあらわすことができます。

$(b_1-a_1)e_r+(b_2-a_2)e_i$

$=\begin{bmatrix} b_1-a_1 \\ b_2-a_2 \\ \end{bmatrix}$

$b_1-a_1$は実軸の成分、$b_2-a_2$は虚軸の成分と考えることができる。

また、複素数平面は虚軸と実軸で構成されています。虚軸は純虚数のみで構成されているため$e_i$を実数倍すると、虚軸を表すことができます。実軸も同様にすることができます。

$e_i$と$e_r$の内積は0になるため、垂直に交わっているので、$e_i$と$e_r$は複素数平面を表すことができます。

$e_i\cdot e_r=0$

だから、複素数平面でもベクトルのような考えをすることができます。