【物理】力の合成と分解の意味と例題について

1. 力の合成と分解
物体に複数の力が働く場合、それらの力を「合成」して一つの力として考えることができます。また、逆に一つの力を複数の方向に分けることを「分解」といいます。
2. 力の合成
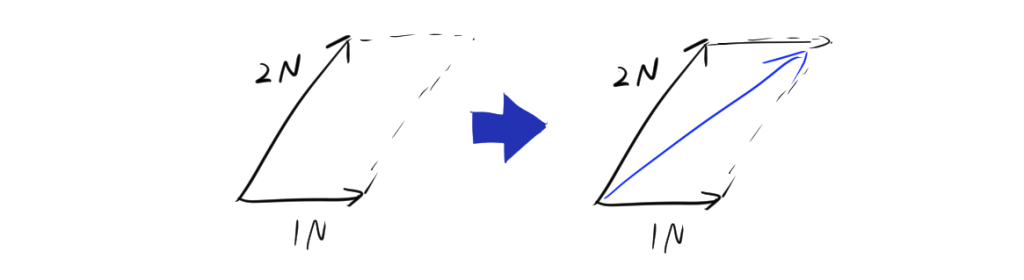
力の合成とは、複数の力を一つの力(合力)として表す操作です。たとえば、異なる方向に働く2つの力がある場合、力はベクトルであるので、ベクトルの加法で考えればその合力を求めることができます。
例えば、次のような1Nと2Nの力が与えられていたとします。ベクトルの加法より、平行四辺形を考えて合力を考えます。
3. 力の分解
力の分解とは、ひとつの力を複数の力に分ける操作のことです。この操作は、最終的に元のベクトルになるようにベクトルを分解したらいいので、様々な分解方法があります。
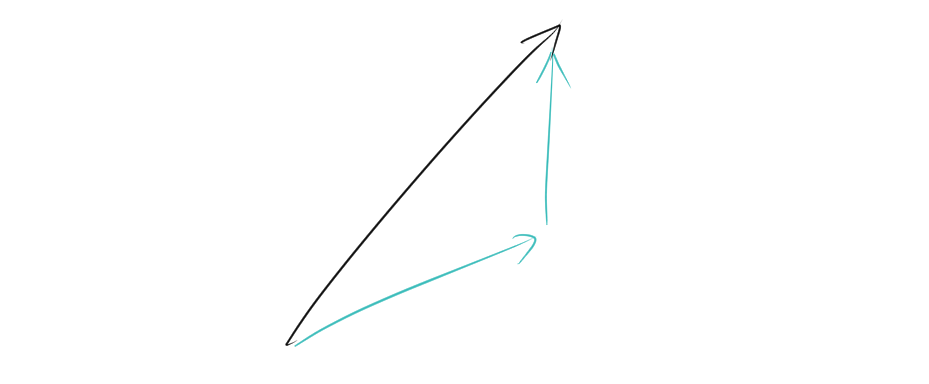
例えば、次のような力(ベクトル)が与えられているとします。
3.1. 2つのベクトルの分解
この力は、以下のように水色で示された2つのベクトルに分解することができます。
3.2. 直交座標
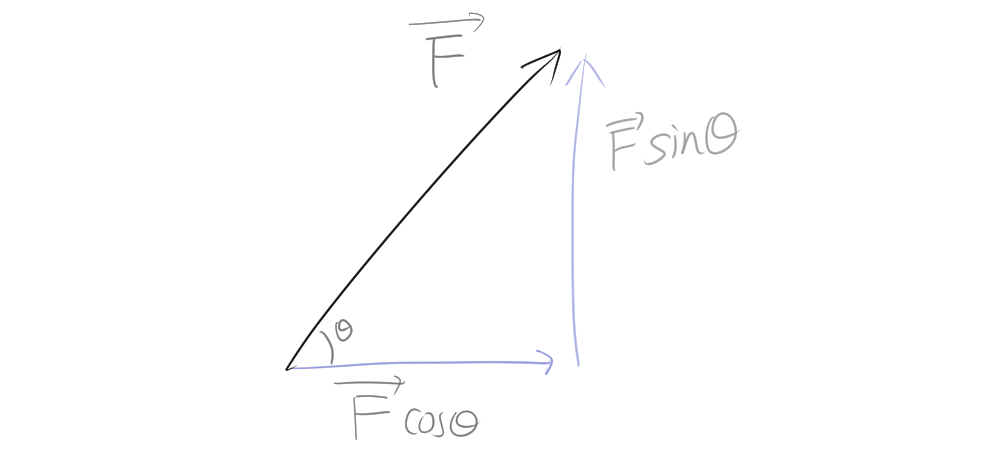
力は垂直方向と水平方向、つまりx軸方向とy軸方向に分解することも可能です。このような場合、ベクトルを \(\overrightarrow{F}\) とすると、次のように分けることができます。
具体的には、\(\overrightarrow{F}\) を角度 \(\theta\) を基準に、x軸方向に \(\overrightarrow{F}\cos\theta\) の力、y軸方向に \(\overrightarrow{F}\sin\theta\) の力に分解することができます。これにより、元のベクトルが二つの直交する力の成分に分かれることになります。
3.3. 大量のベクトル
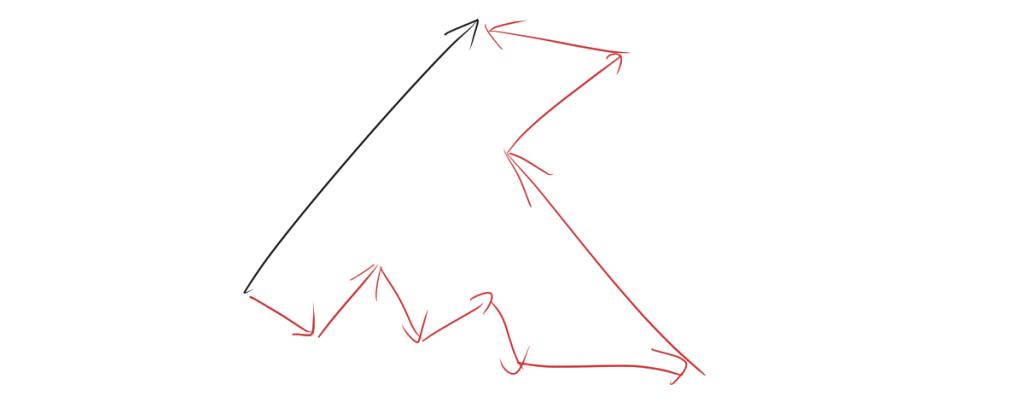
さらに、次の図のように、より多くの方向に力を分解することもできます。
4. 例題
力 \( F = 20\ \text{N} \)、角度 \( \theta = 60^\circ \) ですので、\( \cos 60^\circ = 0.5 \)、\( \sin 60^\circ = \frac{\sqrt{3}}{2} \approx 0.866 \)となります。これを計算すると、
x軸方向の成分 \( F_x \)
\[ F_x = 20 \times \cos 60^\circ = 20 \times 0.5 = 10\ \text{N} \]
y軸方向の成分 \( F_y \)
\[ F_y = 20 \times \sin 60^\circ = 20 \times 0.866 = 17.32\ \text{N} \]