【物理】力のつり合いの意味、例題について

1. 力のつり合いとは?
力のつり合いとは、ある物体に働く全ての力が相殺され、物体が静止したり等速直線運動を続けたりする状態のことを指します。簡単に言えば、物体にかかる力の合計がゼロになるとき、物体はそのままの状態を保つのです。
2. ニュートンの第一法則
ニュートンの第一法則(慣性の法則)によると、「外部から力が加わらなければ、物体は静止し続けるか、等速直線運動を続ける」とされています。つまり、物体に働く力がつり合っていれば、結果的に外力がゼロとなり、物体の運動状態は変化しません。
3. 力のつり合いの具体例
3.1. テーブルの上の本
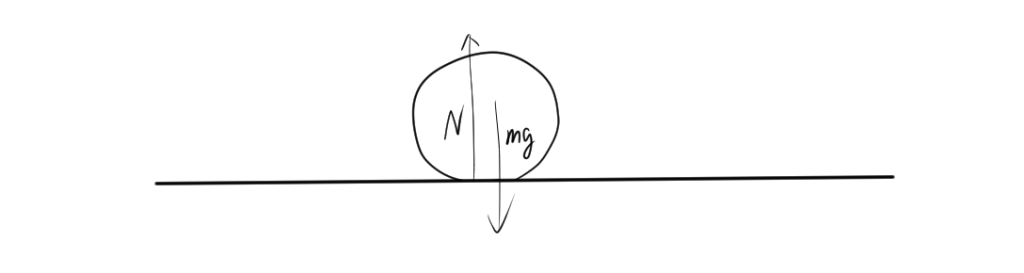
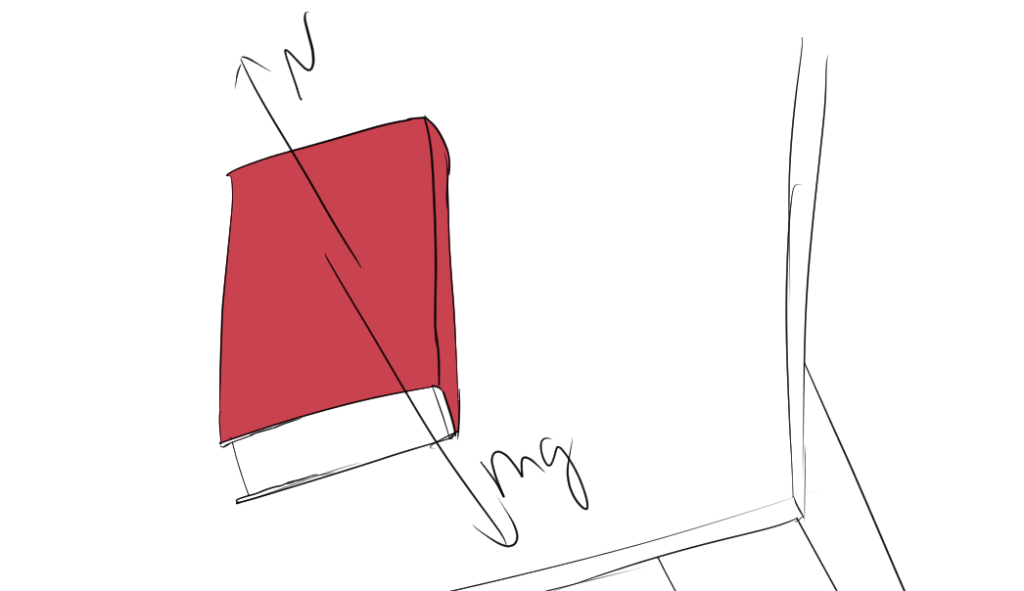
テーブルの上に本を置くと、本は動かずに静止しています。本には地球の重力(下向きの力)が働いていますが、同時にテーブルからの垂直抗力(上向きの力)も働いています。この二つの力が大きさは等しく、向きは反対なので、つり合いが成立し、本は静止します。
3.2. 綱引き
二つのチームが同じ力で綱を引っ張ると、綱は動きません。これは、左右からの引っ張る力が大きさも向きも等しく反対だからです。力がつり合っているため、綱はその場に留まります。
3.3. 天秤
天秤に同じ重さのおもりを両側に乗せると、天秤は水平になります。これは、左右のおもりから働く重力がつり合っているためです。
4. 力のつり合いと直交座標
n個の力が釣り合っている場合、それぞれの力の合力(合計のベクトル)はゼロになります。具体的には、次のように表せます。
ここで、各力 \(\overrightarrow {F_i}\) はベクトルであり、二次元座標で表すと \(\overrightarrow {F_i} = (x_i, y_i)\) となります。この式は、x軸方向とy軸方向のそれぞれで力が釣り合っていることを意味します。まず、x軸方向の力が釣り合っているというのは、全てのx成分を足し合わせるとゼロになることを示しています。すなわち、
$$x_1 + x_2 + \cdots + x_n = 0$$
同様に、y軸方向の力も釣り合っているため、全てのy成分を足し合わせるとゼロになります。
$$y_1 + y_2 + \cdots + y_n = 0$$
このように、力が釣り合うためには、それぞれの成分の合計が0になります。
5. 力のつり合いの例題
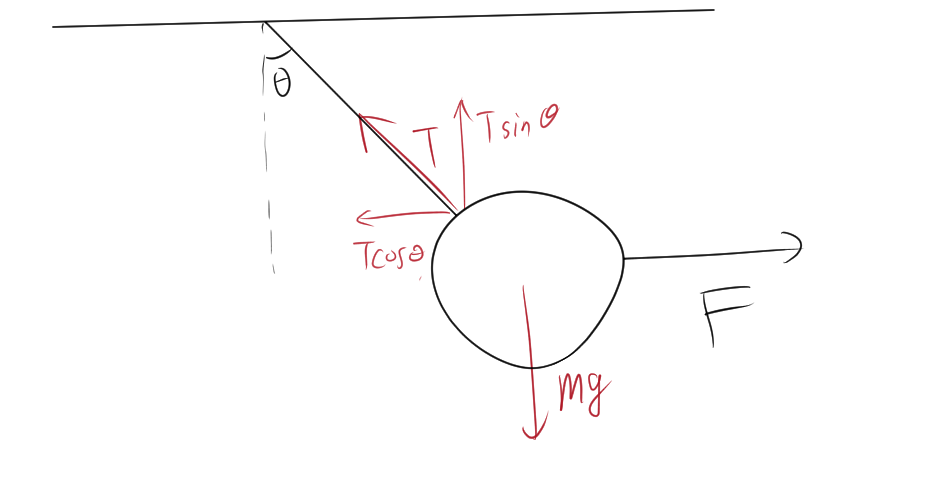
おもりには重力による力が働き、これはおもりの質量 \( m \) と重力加速度 \( g \) によって、重力$mg$が働いています。
糸には張力 \( T \) が生じており、糸が角度 \( \theta \) で傾いているため、この張力は x軸方向と y軸方向に分解できます。張力の x成分 \( T_x \) と y成分 \( T_y \) は、それぞれ次のように表されます。
$$ T_x = T \cos \theta,\, T_y = T \sin \theta $$
釣り合いの条件から、y方向の力の合計はゼロになります。つまり、おもりに働く重力と張力の y成分が釣り合っています。
$$ T \sin \theta =mg $$
また、x方向についても釣り合いが成立するため、x方向の力の合計もゼロです。
$$ T \cos \theta=F $$
ここで、Fを求めると、
\[ \begin{align*} \dfrac{F}{mg} &= \tan \theta \\ F &= mg \tan \theta \end{align*} \]