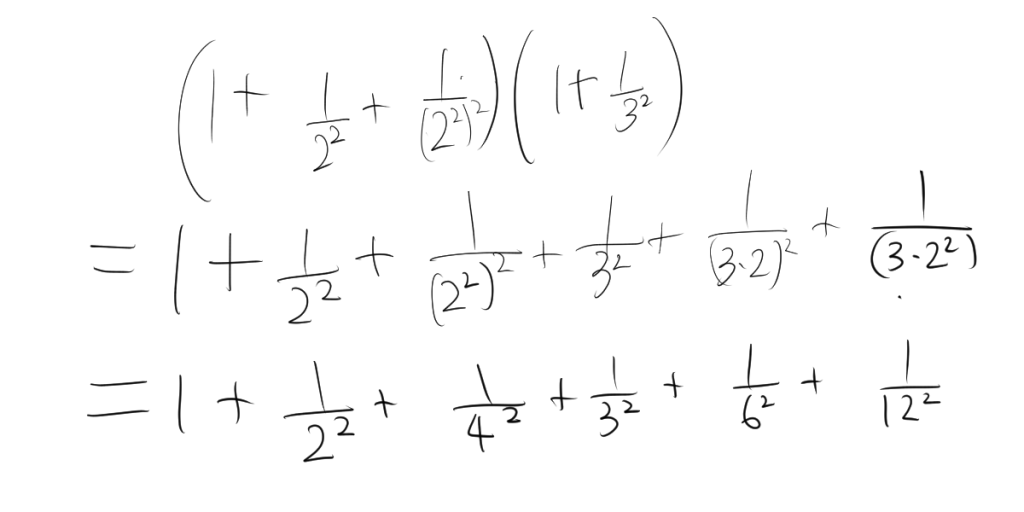互いに素の意味、具体例と性質・確率について
1. 互いに素
「互いに素」（たがいにそ）とは、2つ以上の整数において、それらの整数の最大公約数が1であることを指します。別の言い方をすると、共通する約数が1しかない場合、その2つの整数は「互いに素」であると言います。
例えば、次のペアは互いに素です。
8 と 15 の場合：
8 の約数：1, 2, 4, 8
15 の約数：1, 3, 5, 15
共通する約数は1だけなので、8と15は互いに素です。
一方、12 と 18 の場合：
12 の約数：1, 2, 3, 4, 6, 12
18 の約数：1, 2, 3, 6, 9, 18
共通する約数は1, 2, 3, 6なので、12と18は互いに素ではありません。
2. 互いに素の性質
2.1. 連続する整数
連続する2つの整数 \( n \) と \( n+1 \) が 互いに素ではない と仮定します。つまり、これら2つの数に 1以外の共通の約数 が存在すると仮定します。
その共通の約数を \( d \) とします。すると、\( d \) は 連続する整数の差 \( n+1 – n = 1 \) の約数でもあることになります。つまり、1もdの倍数となります。
しかし、1の約数は 1のみ です。したがって、\( d = 1 \) となります。
これは、連続する2つの整数に共通の約数が1以外の数だと仮定したことに矛盾します。
したがって、連続する2つの整数は 互いに素である ことが証明されました。
実際に互いに素であるか確認してみましょう。
- 4と5 → 最大公約数は1
- 9と10 → 最大公約数は1
連続する整数は常に互いに素であることがわかりました。
2.2. 互いに素になる確率
\[ \lim_{n\to\infty}P_n = \frac{6}{\pi^2} \]
2つの整数 \( a \) と \( b \) が互いに素であるとします。ある素数 \( p \) で割り切れる2つの整数が同時に現れる確率は \( \frac{1}{p^2} \) です。したがって、2つの数が \( p \) で割り切れない（つまり、 \( p \) を共通の因数に持たない）確率は \( 1 – \frac{1}{p^2} \) となります。
2つの整数が互いに素であるためには、どの素数でも両方が同時に割り切れないことが必要です。したがって、全ての素数についての確率を掛け合わせる必要があります。これにより、nが十分に大きいとき、
\[ P_n \approx \prod_{p \text{ は素数}} \left( 1 – \frac{1}{p^2} \right) = \left( 1 – \frac{1}{2^2} \right) \left( 1 – \frac{1}{3^2} \right) \left( 1 – \frac{1}{5^2} \right) \left( 1 – \frac{1}{7^2} \right) \cdots \]
逆数をとると、無限等比級数の公式を利用すると、
\[ \begin{align*} \frac{1}{P_n} &= \frac{2^2}{2^2-1} \frac{3^2}{3^2-1} \frac{5^2}{5^2-1} \frac{7^2}{7^2-1} \cdots \\ &= \frac{1}{1-\frac{1}{2^2}}\frac{1}{1-\frac{1}{3^2}}\frac{1}{1-\frac{1}{5^2}}\frac{1}{1-\frac{1}{7^2}}\cdots \\ &= \left( 1 + \frac{1}{2^2} + \frac{1}{2^4} + \cdots \right) \left( 1 + \frac{1}{3^2} + \frac{1}{3^4} + \cdots \right) \left( 1 + \frac{1}{5^2} + \frac{1}{5^4} + \cdots \right)\cdots \\ &= \sum_{n=1}^{\infty} \frac{1}{n^2}\\ \end{align*} \]
$\sum_{n=1}^{\infty} \frac{1}{n^2}$の形になるのは、分母が素因数分解の形になり、重複がないため。したがって、バーゼル問題の結果から、
$$\lim_{n\to\infty}\frac{1}{P_n} =\frac{\pi^2}{6}$$
今回の証明のポイントは式変形の部分です。特に、$$ \sum_{n=1}^{\infty} \frac{1}{n^2}$$になる部分に着目してみましょう。小さいサイズで考えると次のようになります。
確かに、重複なく、分母が平方数となっていることが確認できます。
