マスジョイ
PR
確率・統計
更新:2024/09/16

例題で解説する指数分布とポアソン分布の違い

はるか
はるか
指数分布とポアソン分布について話すよ。
ふゅか
ふゅか
いいね！急に出てくると忘れちゃうことがあるんだよね！
目次

1. 指数分布とポアソン分布の違い

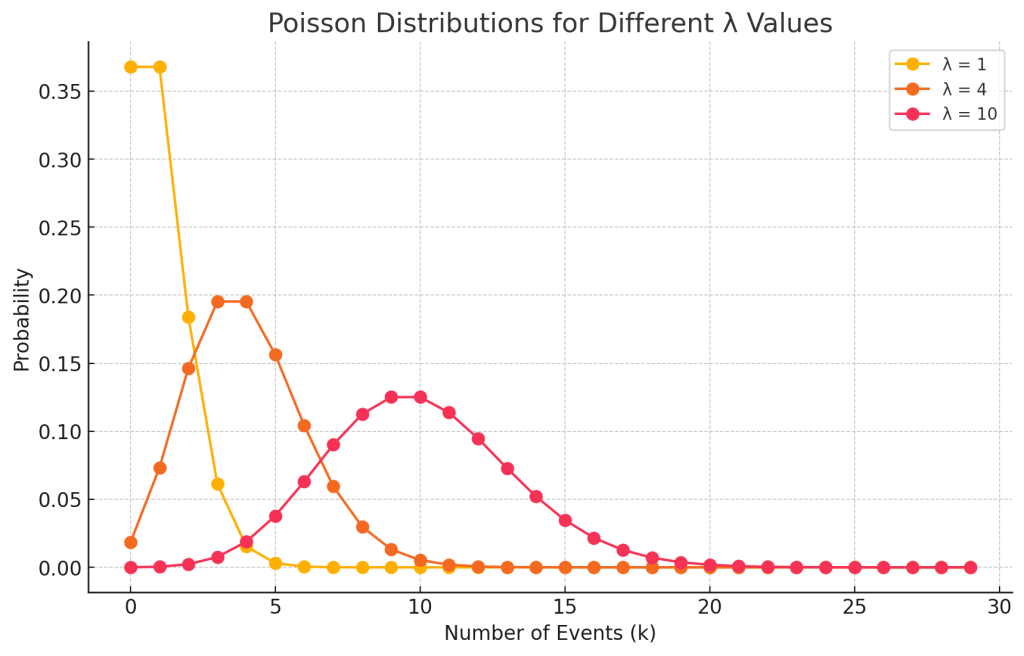
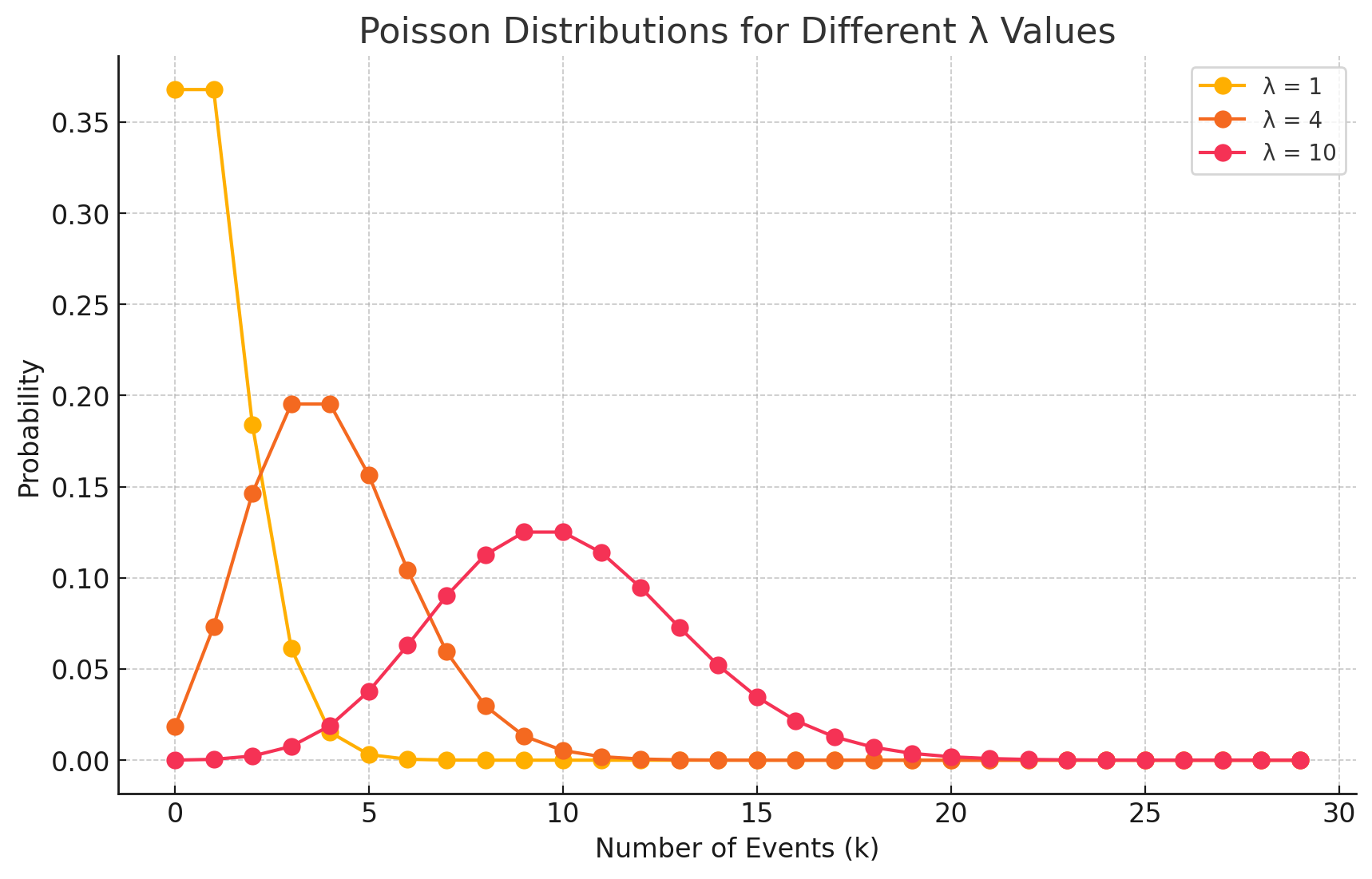
1.1. ポアソン分布 (Poisson Distribution)

  • 確率変数: ポアソン分布の確率変数は、一定の時間または空間内で発生するイベントの回数を表します。この確率変数は離散値を取ります。
  • 例: 1時間内に受ける電話の本数、1日内に到着するメールの数など。


はるか
はるか
ポアソン分布は期間内の回数を扱う分布。

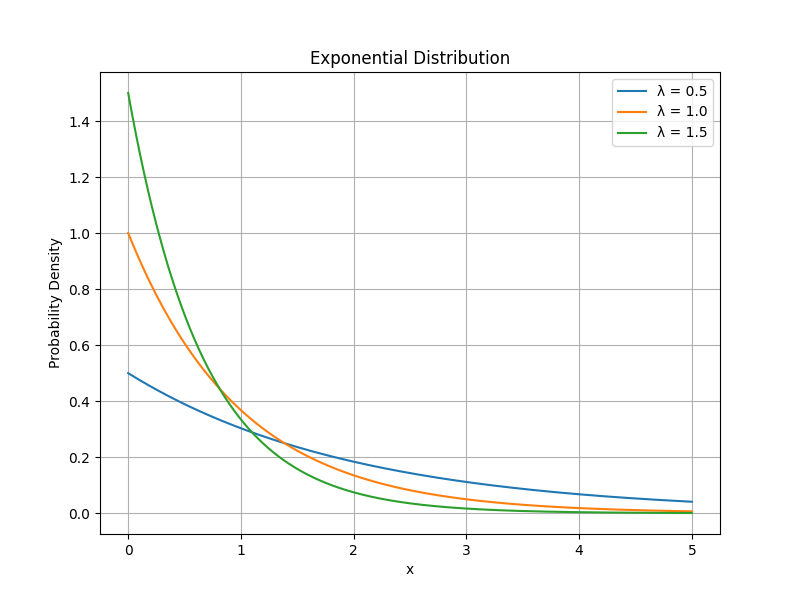
1.2. 指数分布 (Exponential Distribution)

はるか
はるか
次はポアソン分布の例題。ある銀行のATMに1時間あたり平均4人の顧客が訪れる場合だ。
  • 確率変数: 指数分布の確率変数は、連続するイベントの間隔（時間など）を表します。この確率変数は連続値を取ります。
  • 例: 次の電話がかかってくるまでの時間、次のバスが到着するまでの待ち時間など。

指数分布の性質と期待値、分散

はるか
はるか
指数分布はイベントの間隔を扱う分布。

2. 指数分布の例題

ある工場の機械は、平均して1時間に1回故障します。機械が故障するまでの時間は指数分布に従うと仮定します。
  1. 機械が次に故障するまでの時間が2時間以内である確率を求めなさい。
  2. 機械が次に故障するまでの時間が3時間以上かかる確率を求めなさい。

ふゅか
ふゅか
指数分布の例題を見てみよう。ある工場の機械が1時間に1回故障する場合の話だね。

指数分布の確率密度関数は f(t)=λe−λt f(t) = \lambda e^{-\lambda t} であり、累積分布関数は F(t)=1–e−λt F(t) = 1 – e^{-\lambda t} です。ここで、故障率 λ \lambda は 1 時間あたり 1 回です。したがって、λ=1 \lambda = 1 です。

  1. P(T≤2)=F(2)=1–e−2 P(T \leq 2) = F(2) = 1 – e^{-2} P(T≤2)=1–e−2≈1–0.1353=0.8647 P(T \leq 2) = 1 – e^{-2} \approx 1 – 0.1353 = 0.8647 よって、機械が次に故障するまでの時間が2時間以内である確率は約 0.8647 です。
  2. P(T≥3)=1–P(T<3)=1–F(3)=1–(1–e−3) P(T \geq 3) = 1 – P(T < 3) = 1 – F(3) = 1 – (1 – e^{-3}) P(T≥3)=e−3≈0.0498 P(T \geq 3) = e^{-3} \approx 0.0498 よって、機械が次に故障するまでの時間が3時間以上かかる確率は約 0.0498 です。

3. ポアソン分布の例題

ある銀行のATMでは、1時間あたり平均4人の顧客が訪れます。顧客の訪れる数はポアソン分布に従うと仮定します。
  1. 1時間に3人の顧客が訪れる確率を求めなさい。
  2. 1時間に5人以上の顧客が訪れる確率を求めなさい。

はるか
はるか
次はポアソン分布の例題。ある銀行のATMに1時間あたり平均4人の顧客が訪れる場合だ。

ポアソン分布の確率質量関数は P(X=k)=λke−λk! P(X = k) = \dfrac{\lambda^k e^{-\lambda}}{k!} です。ここで、λ=4 \lambda = 4 です。

  1. 1時間に3人の顧客が訪れる確率はP(X=3) P(X = 3) となります。
    P(X=3)=43e−43!=64e−46≈64×0.01836=0.1954 P(X = 3) = \frac{4^3 e^{-4}}{3!} = \frac{64 e^{-4}}{6} \approx \frac{64 \times 0.0183}{6} = 0.1954 よって、1時間に3人の顧客が訪れる確率は約 0.1954 です。
  2. 1時間に5人以上の顧客が訪れる確率P(X≥5)P(X \geq 5)を求めるには、以下のように計算します。P(X≥5)=1–P(X<5)P(X \geq 5) = 1 – P(X < 5) =1–(P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4))= 1 – (P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4))

    まず、各項の確率を計算します。

    P(X=0)=40e−40!=e−4 P(X = 0) = \frac{4^0 e^{-4}}{0!} = e^{-4}

    P(X=1)=41e−41!=4e−4 P(X = 1) = \frac{4^1 e^{-4}}{1!} = 4 e^{-4}

    P(X=2)=42e−42!=8e−4 P(X = 2) = \frac{4^2 e^{-4}}{2!} = 8 e^{-4}

    P(X=3)=43e−43!=64e−46=32e−43 P(X = 3) = \frac{4^3 e^{-4}}{3!} = \frac{64 e^{-4}}{6} = \frac{32 e^{-4}}{3}

    P(X=4)=44e−44!=256e−424=32e−43 P(X = 4) = \frac{4^4 e^{-4}}{4!} = \frac{256 e^{-4}}{24} = \frac{32 e^{-4}}{3}

    これらを合計します。

    P(X<5)=e−4(1+4+8+323+323) P(X < 5) = e^{-4} (1 + 4 + 8 + \frac{32}{3} + \frac{32}{3})

    P(X<5)=e−4(1+4+8+323+323)=e−4(1+4+8+643) P(X < 5) = e^{-4} \left(1 + 4 + 8 + \frac{32}{3} + \frac{32}{3}\right) = e^{-4} \left(1 + 4 + 8 + \frac{64}{3}\right)

    P(X<5)=e−4(13+643)=e−4(393+643)=e−4(1033) P(X < 5) = e^{-4} \left(13 + \frac{64}{3}\right) = e^{-4} \left(\frac{39}{3} + \frac{64}{3}\right) = e^{-4} \left(\frac{103}{3}\right)

    P(X<5)=103e−43 P(X < 5) = \frac{103 e^{-4}}{3}

    最終的に、1時間に5人以上の顧客が訪れる確率は

    P(X≥5)=1–P(X<5)=1–103e−43 P(X \geq 5) = 1 – P(X < 5) = 1 – \frac{103 e^{-4}}{3}

PR
ホームに戻る