度数分布表とヒストグラムの意味と例題について

はるか

度数分布表は、データを整理するための表。データを階級ごとに分けて、その範囲にどれだけのデータがあるかを示す。

ふゅか

そうそう！データの全体的な傾向がわかるのよね！

1. 度数分布表とは

度数分布表は、データを整理して理解しやすくするために用いられる表の一つです。特に、数多くのデータが存在する場合、それらをいくつかの範囲（階級）に分け、その範囲に含まれるデータの個数（度数）を記録します。この表を使うことで、データの分布の様子を視覚的に把握しやすくなります。

1.1. 度数分布表の例

例えば、テストの点数を10点刻みで分類して度数分布表を作成する場合、以下のようになります。

このように、度数分布表を使うことで、どの階級にデータが集中しているのか、またデータの全体的な傾向がわかりやすくなります。

1.2. 度数分布表の用語のまとめ

階級・・・観測データを整理するために、範囲をいくつかの区間に分けたもの。各区間は「階級」と呼ばれ、データがどの範囲に属するかを確認するために使用します。英語だとClass (or Class Interval)。

階級幅・・・階級の幅のこと。各階級がカバーする範囲の差を表します。英語だと、Class Width。

度数・・・各階級に属するデータの個数を表します。度数分布表では、各階級にどれだけのデータが含まれているかが明示されます。英語だとFrequency。

相対度数・・・全体のデータ数に対して、各階級の度数が占める割合を示すもの。英語だとRelative Frequency。

累積相対度数・・・各階級までの相対度数を累積したもの。英語だとCumulative Relative Frequency。

\[ \text{相対度数} = \frac{\text{度数}}{\text{全体のデータ数}} \]

はるか

度数は英語のほうが頻度のfrequencyだから意味がわかりやすい。

2. ヒストグラムとは

ヒストグラムは、度数分布表に基づいてデータの分布を視覚化したグラフです。具体的には、各階級の範囲を横軸に、度数を縦軸に取り、度数に応じた高さの棒（棒グラフ）を描きます。これにより、データの分布や傾向を視覚的に理解することができます。

ふゅか

ヒストグラムって覚えてる？度数分布表のデータをグラフにするやつ！

はるか

うん。階級ごとのデータを棒グラフにする。横軸が階級、縦軸が度数。

2.1. ヒストグラムの作成手順

1. データをいくつかの階級に分けます。
2. 各階級に含まれるデータの個数（度数）を数えます。
3. 横軸に階級、縦軸に度数を設定し、棒グラフを描きます。

2.2. ヒストグラムの例

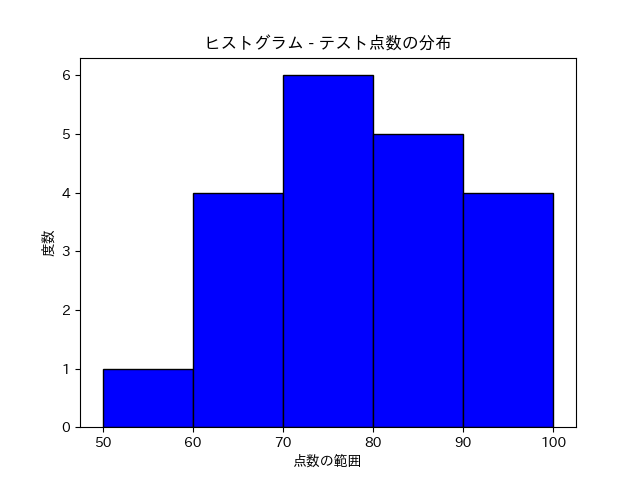
3. 例題

ふゅか

じゃあ、実際に学生のテスト点数を使って度数分布表を作るとして、まずどうする？

はるか

まず、階級幅を決める。今回は10点刻み。次に、各階級に何人いるか数える。

度数分布表

度数分布表をもとにヒストグラムを描きます。