【図解】確率の畳み込みの意味と例題について

1. ベクトルの畳み込みとは
ベクトルの畳み込みは、二つのベクトルを組み合わせてインデックスの和を一定にして、足し合わせて新しいベクトルを生成する数学的な操作です。同様に、ベクトル以外にも、確率や関数の畳み込みでも、和を一定にして足し合わせます。
2. 確率の畳み込みとは
確率の畳み込み(convolution)では、2つの独立な確率変数の和の分布を求めます。具体的には、確率密度関数(PDF)や確率質量関数(PMF)を持つ確率変数 \( X \) と \( Y \) の和 \( Z = X + Y \) の分布を計算する際に使用します。
2.1. 連続確率変数の場合
2.2. 離散確率変数の場合
3. 具体例
3.1. サイコロの例
6面体のサイコロを2つ振るとします。それぞれのサイコロの出目は1から6までの整数で、一様な分布を持っています。このとき、和 \( Z = X + Y \) の分布を求めるには、各サイコロの確率質量関数を畳み込みます。
各サイコロの確率質量関数は
\[ p_X(k) = \begin{cases} \frac{1}{6} & \text{if } k = 1, 2, 3, 4, 5, 6 \\ 0 & \text{otherwise} \end{cases} \]
和の確率質量関数は
\[ p_Z(k) = \sum_{i=1}^{6} p_X(i) p_Y(k – i) \]
計算すると、和の可能な値(2から12)のそれぞれに対して確率を求めることができます。具体的に、和がいくつになるか、そしてその和が発生する組み合わせの数を確認すると、以下のようになります。
- 和が2になる確率:1 + 1 の場合だけ(1通り)
- 和が3になる確率:1 + 2, 2 + 1 の場合(2通り)
- 和が4になる確率:1 + 3, 2 + 2, 3 + 1 の場合(3通り)
- 和が5になる確率:1 + 4, 2 + 3, 3 + 2, 4 + 1 の場合(4通り)
- 和が6になる確率:1 + 5, 2 + 4, 3 + 3, 4 + 2, 5 + 1 の場合(5通り)
- 和が7になる確率:1 + 6, 2 + 5, 3 + 4, 4 + 3, 5 + 2, 6 + 1 の場合(6通り)
- 和が8になる確率:2 + 6, 3 + 5, 4 + 4, 5 + 3, 6 + 2 の場合(5通り)
- 和が9になる確率:3 + 6, 4 + 5, 5 + 4, 6 + 3 の場合(4通り)
- 和が10になる確率:4 + 6, 5 + 5, 6 + 4 の場合(3通り)
- 和が11になる確率:5 + 6, 6 + 5 の場合(2通り)
- 和が12になる確率:6 + 6 の場合だけ(1通り)
各和に対する確率は、該当する和の組み合わせ数を全組み合わせ(36通り)で割った値になります。つまり、\( p_Z(k) \) を求めると次のようになります。
\[ p_Z(k) = \frac{\text{組み合わせの数}}{36} \]
具体的な値は以下の通りです。
- \( p_Z(2) = \frac{1}{36} \)
- \( p_Z(3) = \frac{2}{36} = \frac{1}{18} \)
- \( p_Z(4) = \frac{3}{36} = \frac{1}{12} \)
- \( p_Z(5) = \frac{4}{36} = \frac{1}{9} \)
- \( p_Z(6) = \frac{5}{36} \)
- \( p_Z(7) = \frac{6}{36} = \frac{1}{6} \)
- \( p_Z(8) = \frac{5}{36} \)
- \( p_Z(9) = \frac{4}{36} = \frac{1}{9} \)
- \( p_Z(10) = \frac{3}{36} = \frac{1}{12} \)
- \( p_Z(11) = \frac{2}{36} = \frac{1}{18} \)
- \( p_Z(12) = \frac{1}{36} \)
このようにして、サイコロ2つの和の分布が得られます。
3.2. 一様分布と一様分布の畳み込みの確率密度関数
| 項目 | 内容 |
|---|---|
| 確率変数 | \(X,Y\) ― 独立・同分布 |
| 分布 | 一様分布 \(U(0,9)\) |
| \(f_X(x)=f_Y(x)=\dfrac19\,1_{[0,9]}(x)\) | |
| 目的 | \(Z=X+Y\) の pdf \(f_Z(z)\) を求める |
畳み込み積分の立式
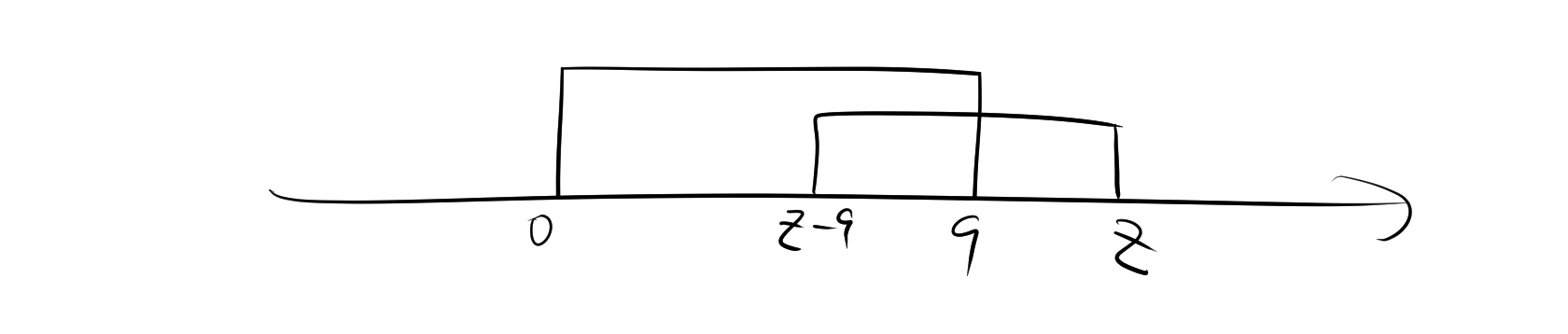
\[ f_Z(z) =\int_{-\infty}^{\infty}f_X(x)\,f_Y(z-x)\,dx\]
- \(x\) は 0–9 で有効
- \(z-x\) も 0–9 で有効 \(\Longrightarrow\;z-9\le x\le z\)
この 2 本の不等式を同時に満たす 実際の積分区間は \(z\) の値で変わるため,区分して計算する。
3.2.1. ケース A \(z<0\)
和z=x+yが負になることはない(範囲外) → \(f_Z(z)=0\)
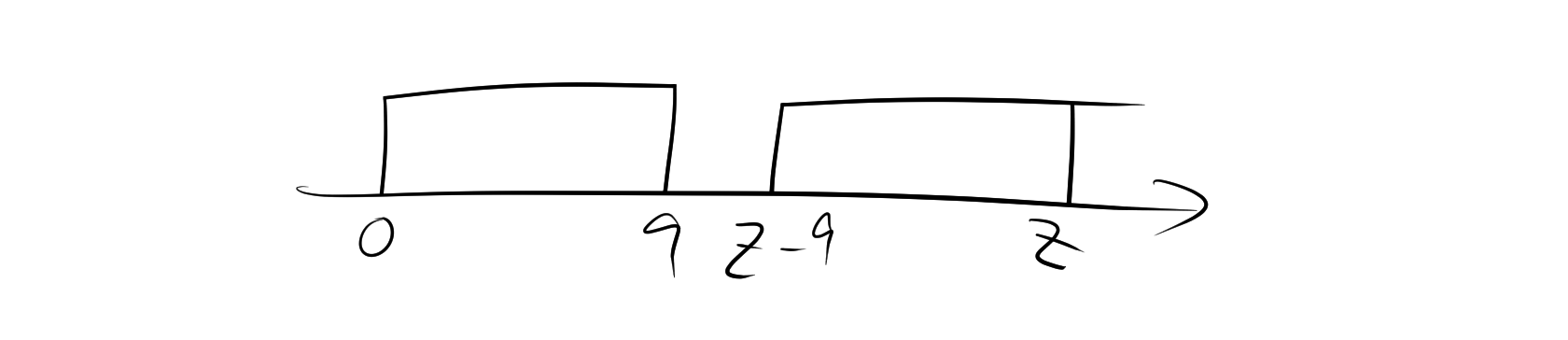
3.2.2. ケース B \(0\le z\le 9\)
\[ f_Z(z) =\frac1{81}\int_{0}^{z}dx =\frac{z}{81} \]
3.2.3. ケース C \(9< z\le 18\)
\[ f_Z(z) =\frac1{81}\int_{z-9}^{9}dx =\frac{18-z}{81} \]
3.2.4. ケース D \(z>18\)
和は18以上になることはない。→ \(f_Z(z)=0\)
3.2.5. 結果のまとめ
\[ \boxed{\,f_Z(z)= \begin{cases} \dfrac{z}{81} & 0\le z\le9\\[6pt] \dfrac{18-z}{81} & 9<z\le18\\[6pt] 0 & \text{その他} \end{cases}} \]