調和級数の定義・性質・オイラー定数について
1. 調和級数とは
\[ \lim_{n \to \infty }\sum_{k=1}^{n} \frac{1}{k} = 1 + \frac{1}{2} + \frac{1}{3} + \dots \]
2. 調和級数の性質
2.1. オイラー・マスケローニ定数
オイラー・マスケローニ定数$\gamma $は次のように定義されます。
\[ \gamma = \lim_{n \to \infty} \left( \sum_{k=1}^{n} \frac{1}{k} - \ln n \right) \]
値は約 \( \gamma \approx 0.57721 \) です。調和級数の部分和の増加が対数的に増加することを示している。
2.2. 調和級数が発散する証明1（面積）
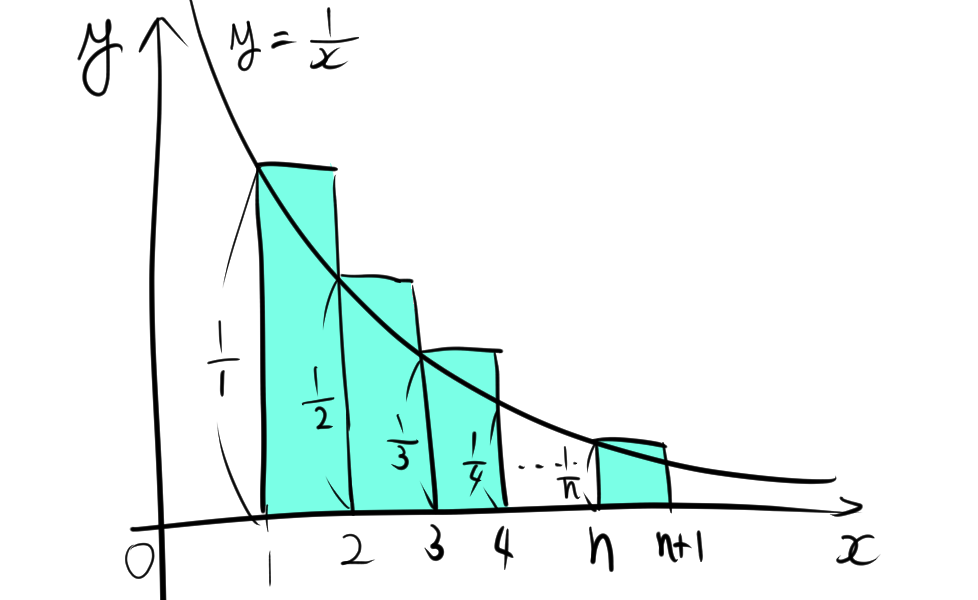図より、面積の大きさを比較した不等式を立てると次のようになる。
$$\int^{n+1}_1 \frac{1}{x}\leq\sum^{n}_{k=1}\frac{1}{k}$$
$$\therefore\log(n+1)\leq\sum^{n}_{k=1}\frac{1}{k}$$
したがって、$n\to\infty$とすると、左辺が発散するため、調和級数も発散する。
2.3. 調和級数が発散する証明2 (マクローリン展開を利用)
マクローリン展開の由来の不等式$e^x\geq x +1$を利用して調和級数が発散することを証明します。まず、調和級数の部分和を次のように定義します。
\[ H_n = \sum_{k=1}^{n} \frac{1}{k} \]
次に、与えられた式を基にして、調和級数の部分和が対数関数で下から抑えられることを示します。与えられた式を整理すると、
\[ \exp\left(H_n\right) =\exp\left(\sum_{k=1}^{n} \frac{1}{k}\right) = \exp(1) \exp\left(\frac{1}{2}\right) \exp\left(\frac{1}{3}\right) \cdots \exp\left(\frac{1}{n}\right) \]
\[ = \prod_{k=1}^{n} \exp\left(\frac{1}{k}\right) \]
\[ \geq \prod_{k=1}^{n} \left(1 + \frac{1}{k}\right) \]
\[ = \left(1 + \frac{1}{1}\right) \left(1 + \frac{1}{2}\right) \left(1 + \frac{1}{3}\right) \cdots \left(1 + \frac{1}{n}\right) \]
\[ = 2 \frac{3}{2}\frac{4}{3}\dots\frac{n+1}{n}=n+1 \]
したがって、
\[ \exp(H_n) \geq n + 1 \]
ここで、両辺の対数を取ると、
\[ H_n \geq \log(n + 1) \]
したがって、$n\to\infty$とすると、右辺が発散するため、調和級数も発散する。
