数列の上極限（lim sup）と下極限（lim inf）の意味と具体例について

数列は 1 点に落ち着く（収束する）ものばかりではありません。

• 1, −1, 1, −1,… のように 振動 したり
• 1, 2, 3, 4,… のように 発散 したり

──そんな「行き先が定まらない」数列を相手にするとき役に立つのが 上極限 (limsup) と 下極限 (liminf) です。

ざっくり言えば、 “数列の尻尾（後半部分）” だけ見て決める道具です。

はるか

数列って全部が1つの値に落ち着くわけじゃない。

ふゅか

そうそう！例えば1, -1, 1, -1, …みたいにずっと振動するのもあるし、1, 2, 3, 4, …みたいにどんどん大きくなるのもあるわね！

はるか

そんなとき便利なのが、上極限と下極限。

1. 上極限（lim sup）の意味

2. 下極限（lim inf）の意味

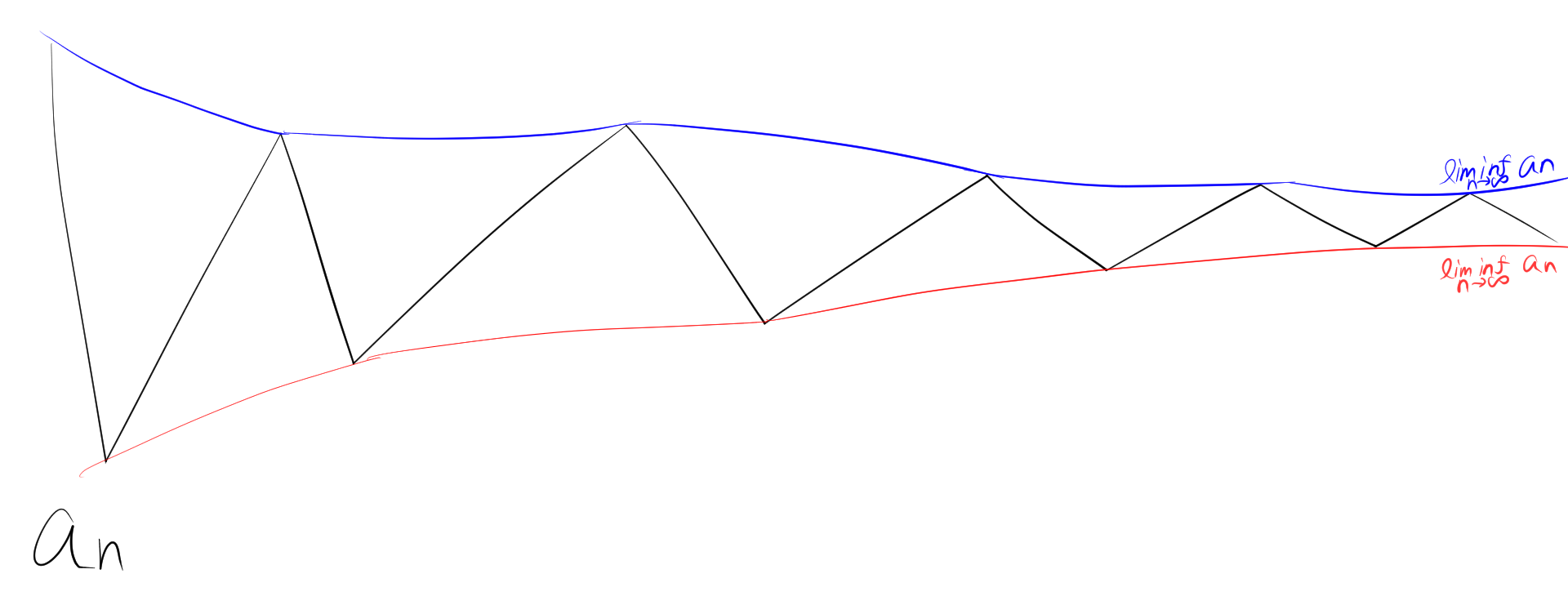
3. 図でイメージ

4. 例題

上極限（limsup）と下極限（liminf）の考え方を理解するために、いくつか具体的な数列を例に挙げて確認してみましょう。

4.1. 例1. 数列 \(a_n = (-1)^n\)

この数列は、1, -1, 1, -1, 1, -1, … というように、値が交互に1と-1を繰り返す数列です。つまり、値が一定の範囲内で激しく振動しています。

• 上極限（limsup）：1
• 下極限（liminf）：-1

このように、振動する数列では「一番大きい値」が上極限、「一番小さい値」が下極限となります。

4.2. 例2. 数列 \(a_n = \frac{1}{n}\)

この数列は、1, 1/2, 1/3, 1/4, 1/5, … と進むごとに値がどんどん小さくなり、最終的には0に近づいていきます。

この場合は、数列が収束しているので、上極限も下極限も同じ値になります。

• 上極限（limsup）：0
• 下極限（liminf）：0

このように、収束する数列では、その収束先の値が上極限・下極限どちらにもなります。

4.3. 例3. 数列 \(a_n = \sin n\)

この数列は、nの値が増えるごとに sin の値が変化していくものです。sin の値は -1〜1 の範囲に収まりますが、n を大きくしても周期的に様々な値を取り続けます。収束はしませんが、取る値の範囲は決まっています。

• 上極限（limsup）：1
• 下極限（liminf）：-1

sin の特性により、どこまで進んでも「最大値は1」「最小値は-1」となります。

4.4. 例4. 数列 \(a_n = \cos n\)

この数列も sin と同じように、cos の値を次々と取っていくものです。cos の値も -1〜1 の範囲で動きます。周期的に変化し、発散することはありません。

• 上極限（limsup）：1
• 下極限（liminf）：-1

sin と同様に、取る値の最大・最小が決まっているので、このような結果になります。

5. まとめ表

最後に、上で紹介した4つの数列について、上極限・下極限をまとめた表を用意しました。数列の特徴とあわせて確認しておきましょう。