双曲線関数の加法定理の証明と例題について

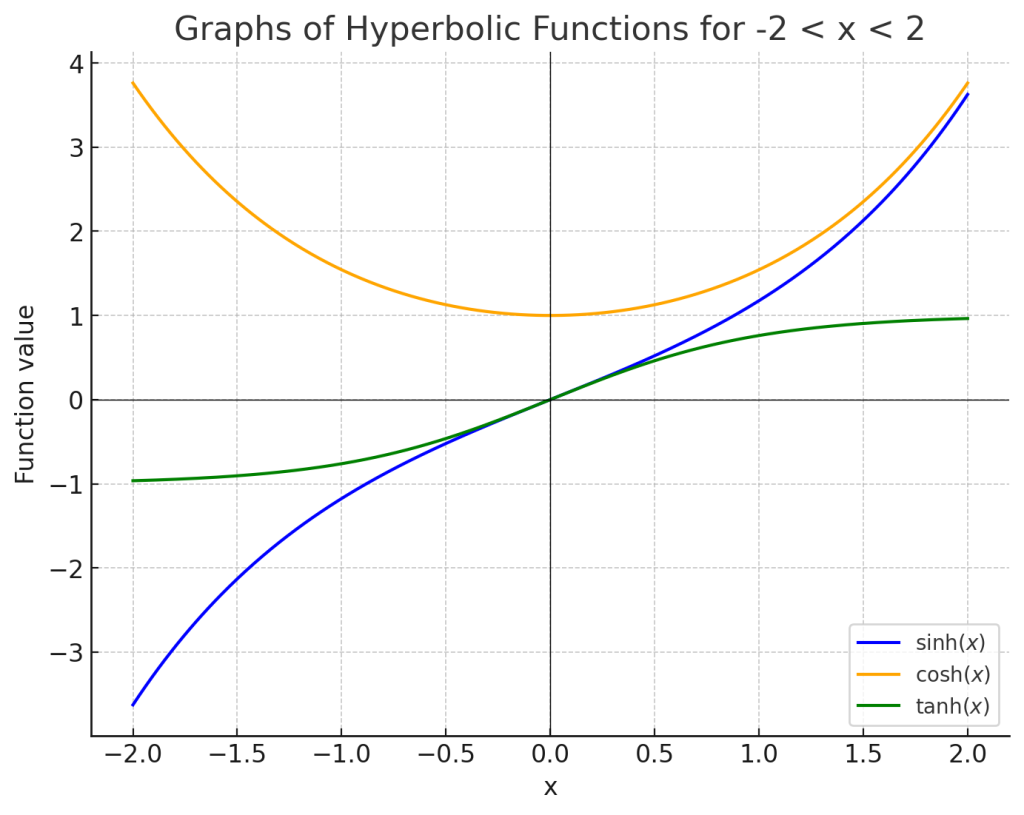
1. 双曲線関数とは
\[ \sinh(x) = \frac{e^x – e^{-x}}{2} \]
\[ \cosh(x) = \frac{e^x + e^{-x}}{2} \]
\[ \tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^x – e^{-x}}{e^x + e^{-x}} \]
2. 双曲線関数の加法定理
2.1. 加法定理
ほとんど三角関数の加法定理と同じですが、符号が異なります。三角関数の加法定理とは異なり双曲線関数の加法定理は符号は一致しています。
$$\large1.\sinh \left( x+y\right) =\sinh x\cosh y+\sinh y\cosh x$$
$$\large2.\sinh \left( x-y\right) =\sinh x\cosh y-\sinh y\cosh x$$
$$\large3.\cosh \left( x+y\right) =\cosh x\cosh y+\sinh x\sinh y$$
$$\large4.\cosh \left( x-y\right) =\cosh x\cosh y-\sinh x\sinh y$$
$$\large5.\tanh \left( x+y\right) =\frac{\tanh x+\tanh y}{1+\tanh x\tanh y}$$
$$\large6.\tanh \left( x-y\right) =\frac{\tanh x-\tanh y}{1-\tanh x\tanh y}$$
2.2. 計算による証明
\(\Large\cosh x=\frac{e^{x}+e^{-x}}{2},\sinh x=\frac{e^{x}-e^{-x}}{2},\tanh x=\frac{\sinh x}{\cosh x}\)を用いる。
2.3. 加法定理1の証明
右辺から左辺を導きます。
$$\Large\sinh x\cosh y+\sinh y\cosh x$$
$$\Large=\frac{\left( e^{x}+e^{-x}\right) }{2}\cdot \frac{\left( e^{y}-e^{-y}\right) }{2}+\frac{\left( e^{x}-e^{-x}\right) }{2}\cdot \frac{\left( e^{y}+e^{-y}\right) }{2}$$
$$\Large=\frac{2\left( e^{x+y}+e^{-x-y}\right) }{4}$$
$$\Large=\frac{e^{x+y}+e^{-x-y}}{2}$$
$$\Large=\sinh \left( x+y\right) $$
左辺と一致している。
2.4. 加法定理3の証明
$$\Large\cosh x\cosh y+\sinh x\sinh y$$
$$\Large=\frac{\left( e^{x}+e^{-x}\right) }{2}\cdot \frac{\left( e^{y}+e^{-y}\right) }{2}+\frac{\left( e^{x}-e^{-x}\right) }{2}\cdot \frac{\left( e^{y}-e^{-y}\right) }{2}$$
$$\Large=\frac{2\left( e^{x+y}-e^{-x-y}\right) }{4}$$
$$\Large=\frac{e^{x+y}-e^{-x-y}}{2}$$
$$\Large=\cosh \left( x+y\right) $$
左辺と一致している。
2.5. 加法定理5の証明
1、3を\(tanh(x+y)\)に代入すると、
$$\Large\tanh (x+y)$$
$$\Large=\frac{\sinh (x+y)}{\cosh (x+y)}\\$$
$$\Large=\frac{\cosh x\sinh y+\cosh y\sinh x}{\cosh x\cosh y+\sinh x\sinh y}$$
分子分母を\(\cosh x\cosh y\)で割ると
$$\Large =\frac{\tanh x+\tanh y}{1+\tanh x\tanh y}$$
2.6. 加法定理2,4,6の証明
三角関数と同様に\(y\)を\(-y\)と考えれば2.4.6は証明できます。
3. 双曲線関数の加法定理の例題
3.1. 例題1:\(\sinh(2x)\)
\[ \sinh(2x) = 2 \sinh(x) \cosh(x) \]
双曲線関数の加法定理を使います。
\[ \sinh(2x) = \sinh(x + x) \]
\[ = \sinh(x)\cosh(x) + \cosh(x)\sinh(x) \]
\[ \therefore \sinh(2x) = 2\sinh(x)\cosh(x) \]
双曲線関数の加法定理を使って、\(\sinh(2x) = 2\sinh(x)\cosh(x)\) が証明されました。
3.2. 例題2:$\cosh(2x)$
\[ \cosh(2x) = \cosh^2(x) + \sinh^2(x) \]
双曲線関数の加法定理を使います。
\[ \cosh(2x) = \cosh(x + x) \]
\[ \cosh(2x) = \cosh(x)\cosh(x) + \sinh(x)\sinh(x) \]
\[ \cosh(2x) = \cosh^2(x) + \sinh^2(x) \]
双曲線関数の加法定理を使って、\(\cosh(2x) = \cosh^2(x) + \sinh^2(x)\) が証明されました。
3.3. 例題3:$\sinh(3x)$
\ \[ \sinh(3x) = 3\sinh(x) + 4\sinh^3(x) \]
\(\sinh(3x)\) を求める際に、まず \(\sinh(2x)\) の結果を利用して計算してみましょう。
\(\sinh(3x)\) は \(\sinh(2x + x)\) として表すことができます。双曲線関数の加法定理を使用します。
\[ \sinh(3x) = \sinh(2x + x) = \sinh(2x)\cosh(x) + \cosh(2x)\sinh(x) \]
\(\sinh(2x) = 2\sinh(x)\cosh(x)\) を代入します。
\[ \sinh(3x) = [2\sinh(x)\cosh(x)]\cosh(x) + \cosh(2x)\sinh(x) \]
\[ \sinh(3x) = 2\sinh(x)\cosh^2(x) + \cosh(2x)\sinh(x) \]
\(\cosh(2x) = \cosh^2(x) + \sinh^2(x)\) を代入します。
\[ \sinh(3x) = 2\sinh(x)\cosh^2(x) + (\cosh^2(x) + \sinh^2(x))\sinh(x) \]
\[ \sinh(3x) = 2\sinh(x)\cosh^2(x) + \sinh(x)\cosh^2(x) + \sinh^3(x) \]
\[ \sinh(3x) = 3\sinh(x)\cosh^2(x) + \sinh^3(x) \]
双曲線関数の関係式を利用して \(\cosh^2(x) = 1 + \sinh^2(x)\) を代入します。
\[ \sinh(3x) = 3\sinh(x)(1 + \sinh^2(x)) + \sinh^3(x) \]
\[ \sinh(3x) = 3\sinh(x) + 3\sinh^3(x) + \sinh^3(x) \]
\[ \sinh(3x) = 3\sinh(x) + 4\sinh^3(x) \]