【図解】素数定理とは？素数の個数に関連する定理とグラフについて

$はるか$

はるか

素数定理って簡単に言うと何？

$ふゅか$

ふゅか

素数の分布を示したすごい定理なんだよ！

1. 素数定理

素数定理は、整数 1以上$ n $ 以下の素数の個数を表す関数 $ \pi(n) $は、$ n $ が十分に大きいとき、

\[ \pi(n) \sim \frac{n}{\log n} \]

つまり、整数 $ n $ 以下に存在する素数の個数 $ \pi(n) $ は、$ \frac{n}{\log n} $ に非常に近づくということです。より正確には、

\[ \lim_{n \to \infty} \frac{\pi(n) \log n}{n} = 1 \]

という形で素数の分布が表されます。

$ふゅか$

ふゅか

実際にグラフにしてみてみよう！

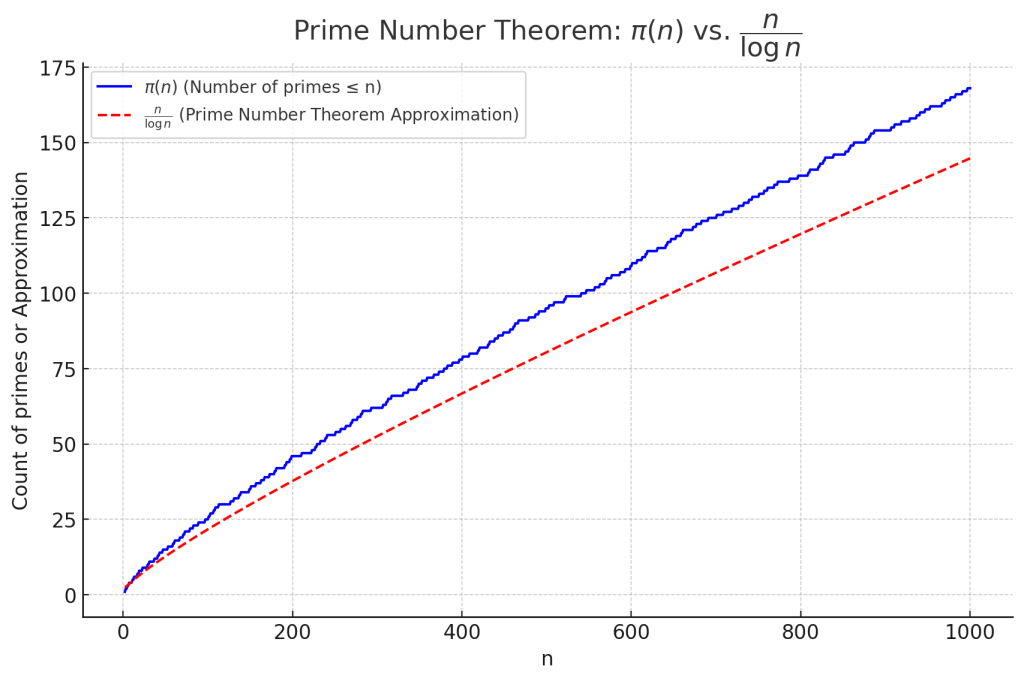
素数定理に基づく $ n $ 以下の素数の個数 $\pi(n)$ と、その近似値 $\frac{n}{\log n}$ の関係をグラフにすると、

青い実線 ($\pi(n)$)・・・この線は $ n $ 以下の素数の正確な個数を表しています。
赤い破線 ($\frac{n}{\log n}$)・・・この線は素数定理による近似値です。素数定理によれば、整数 $ n $ が非常に大きくなるにつれて、素数の個数 $\pi(n)$ は $\frac{n}{\log n}$ に近づいていきます。