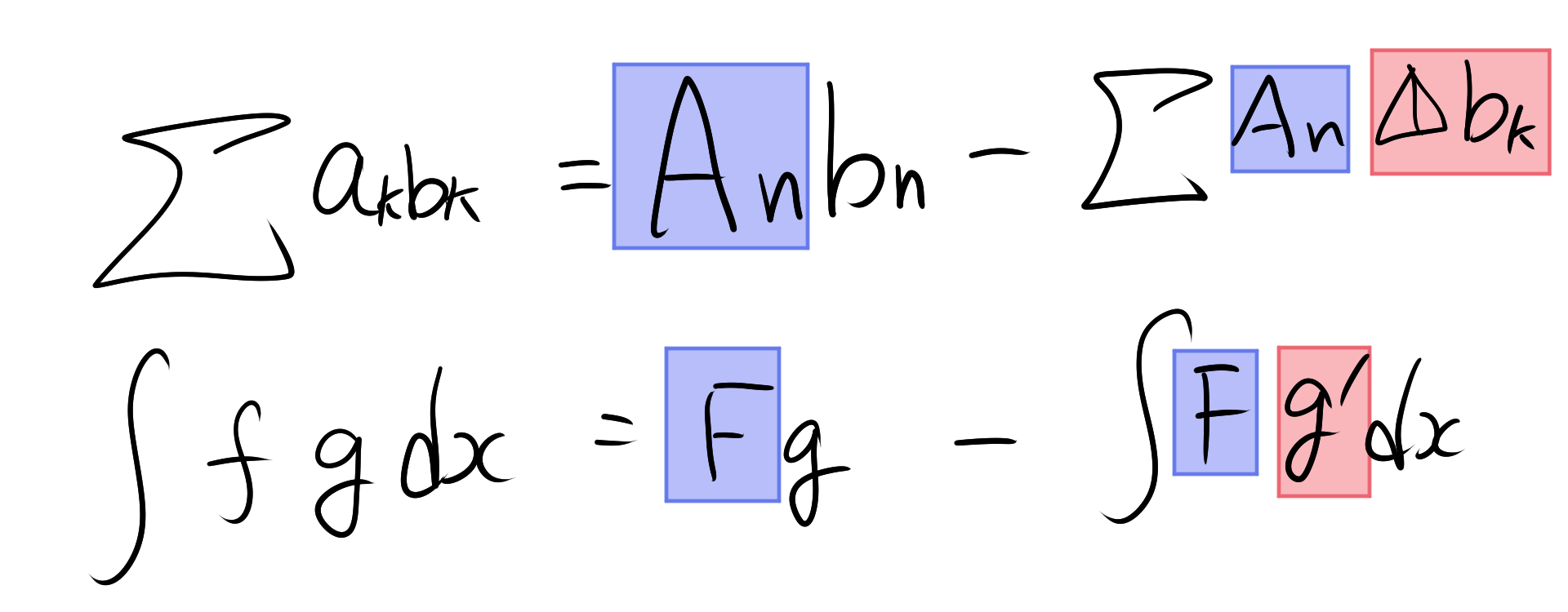アーベルの総和公式の意味と証明について

1. アーベルの総和公式

アーベルの総和公式は、数列 \( \{a_k\} \) と \( \{b_k\} \) の積の和を、部分和 \( A_k \) と数列 \( b_k \) に基づいて分解する公式です。

1.1. アーベルの総和公式のイメージ

アーベルの総和公式は部分積分と非常に似ています。

積分を部分和、差分を微分と考えれば対応しているように見えます。そう、直感的には部分積分の離散版の計算していイメージになります。

実際に、部分積分を離散化してみましょう。

$$\int fg \, dx = Fg-\int F g’ \, dx$$

積分を部分和、差分を微分として考えると

$$\sum f(k)g(k)  = F(n)g(n)-\sum F(k)(g(k+1)-g(k))$$

2. 具体例

与えられた式を具体的な \( n \) の値で計算してみましょう。

2.1. \( n = 1 \) の場合

• 左辺： \[ \sum_{k=1}^1 a_k b_k = a_1 b_1 \]
• 右辺： \[ A_1 b_1 – \sum_{k=1}^0 A_k (b_{k+1} – b_k) \] ここで \( A_1 = a_1 \) であり、\( \sum_{k=1}^0 \) は 0 です。 よって右辺は： \[ a_1 b_1 \] 結果として \( n = 1 \) の場合、左辺 = 右辺 となります。

2.2. \( n = 2 \) の場合

• 左辺： \[ \sum_{k=1}^2 a_k b_k = a_1 b_1 + a_2 b_2 \]
• 右辺： \[ A_2 b_2 – \sum_{k=1}^1 A_k (b_{k+1} – b_k) \] ここで \( A_1 = a_1 \), \( A_2 = a_1 + a_2 \) です。 よって右辺は： \[ \begin{align*} & (a_1 + a_2)b_2 – a_1 (b_2 – b_1) \\ &= a_1 b_2 + a_2 b_2 – \left( a_1 b_2 – a_1 b_1 \right) \\ &= a_1 b_2 + a_2 b_2 – a_1 b_2 + a_1 b_1 \\ &= a_1 b_1 + a_2 b_2 \end{align*}\] これにより、左辺 = 右辺 が確認できます。

2.3. \( n = 3 \) の場合

• 左辺： \[ \sum_{k=1}^3 a_k b_k = a_1 b_1 + a_2 b_2 + a_3 b_3 \]
• 右辺： \[ A_3 b_3 – \sum_{k=1}^2 A_k (b_{k+1} – b_k) \] ここで \( A_1 = a_1 \), \( A_2 = a_1 + a_2 \), \( A_3 = a_1 + a_2 + a_3 \) です。 右辺を展開すると：
  $$\begin{align*} & (a_1 + a_2 + a_3)b_3 – \lbrace a_1(b_2 – b_1) + (a_1 + a_2)(b_3 – b_2) \rbrace \\ &= a_1 b_3 + a_2 b_3 + a_3 b_3 – \lbrace  a_1 b_2 – a_1 b_1 + a_1 b_3 + a_2 b_3 – a_2 b_2 \rbrace \\ &= a_1 b_3 + a_2 b_3 + a_3 b_3 – a_1 b_2 + a_1 b_1 – a_1 b_3 – a_2 b_3 + a_2 b_2 \\ &= a_1 b_1 + a_2 b_2 + a_3 b_3 \end{align*}$$
  これにより、左辺 = 右辺 が確認できます。

3. アーベルの総和公式の証明

3.1. 式変形で求める方法

数列 \( A_k = \displaystyle\sum_{i=1}^k a_i \) を用いると、\( a_k = A_k – A_{k-1} \) と表せます。これを利用すると、

\[ \sum_{k=1}^n a_k b_k = (A_1)b_1 + (A_2 – A_1)b_2 + \cdots + (A_n – A_{n-1})b_n \]

各項を分解してまとめると

\[ \sum_{k=1}^n a_k b_k = A_1 b_1 + A_2 b_2 – A_1 b_2 + A_3 b_3 – A_2 b_3 + \cdots + A_n b_n – A_{n-1} b_n \]

ここで、$A_k$で項をまとめると、

\[\begin{align*} \sum_{k=1}^n a_k b_k &= A_1 (b_1 – b_2) + A_2 (b_2 – b_3) + \cdots + A_{n-1} (b_{n-1} – b_n) + A_n b_n \\ &= A_n b_n + \sum_{k=1}^{n-1} A_k (b_{k} – b_{k+1}) \\ &= A_n b_n – \sum_{k=1}^{n-1} A_k (b_{k+1} – b_k) \end{align*}\]

3.2. 数学的帰納法を利用した証明

数学的帰納法を利用して、アーベルの総和公式を証明してみましょう。

\( n = 1 \) の場合

\[ \sum_{k=1}^1 a_k b_k = a_1 b_1 \]

\[ A_1 b_1 – \sum_{k=1}^0 A_k (b_{k+1} – b_k) \]

ここで \( A_1 = a_1 \) であり、\( \sum_{k=1}^0 \) は \( 0 \) です。したがって、

\[ A_1 b_1 – \sum_{k=1}^0 A_k (b_{k+1} – b_k)=a_1 b_1 \]

したがって、左辺 = 右辺 が成り立ちます。

\( n = 1 \) の場合に成立することが確認できました。

\( n = m \) の場合に

\[ \sum_{k=1}^m a_k b_k = A_m b_m – \sum_{k=1}^{m-1} A_k (b_{k+1} – b_k) \]

が成り立つとします。

\( n = m+1 \) の場合、左辺は

\[ \sum_{k=1}^{m+1} a_k b_k = \left( \sum_{k=1}^m a_k b_k \right) + a_{m+1} b_{m+1} \]

仮定を使うと、左辺は

\[ \sum_{k=1}^{m+1} a_k b_k = \left( A_m b_m – \sum_{k=1}^{m-1} A_k (b_{k+1} – b_k) \right) + a_{m+1} b_{m+1} \]

ここで、\( a_{m+1}= A_{m+1} – A_m \) であることから、

\[ \begin{align*} &= \left( A_m b_m – \sum_{k=1}^{m-1} A_k (b_{k+1} – b_k) \right) + a_{m+1} b_{m+1} \\ &= \left( A_m b_m – \sum_{k=1}^{m-1} A_k (b_{k+1} – b_k) \right) +(A_{m+1} – A_m )b_{m+1} \\ &=  A_m( b_m -b_{m+1})- \sum_{k=1}^{m-1} A_k (b_{k+1} – b_k) +A_{m+1} b_{m+1} \\ &=A_{m+1} b_{m+1}-A_m( b_{m+1}-b_m )- \sum_{k=1}^{m-1} A_k (b_{k+1} – b_k) \\ &=A_{m+1} b_{m+1}- \sum_{k=1}^{m} A_k (b_{k+1} – b_k) \end{align*} \]

これにより、仮定が \( n = m+1 \) の場合にも成り立つことが確認できます。

\( n = 1 \) の場合に成立し、\( n = m \) の場合に成立すると仮定して \( n = m+1 \) の場合に成立することを示したので、数学的帰納法より任意の \( n \) に対して与えられた式が成り立つことが証明された。

4. 計算例

4.1. 数列の例

次の数列に対してアーベルの総和公式を適応します。

• \( a_k = \dfrac{1}{k} \)
• \( b_k = k \)

4.2. 実際の計算

部分和 \( A_k \) を計算します。

\[ A_k = \sum_{i=1}^k \frac{1}{i} \]

差分 \( b_{k+1} – b_k \) を計算すると、

\[ b_{k+1} – b_k = (k+1) – k = 1 \]

公式を適用すると

\[ \sum_{k=1}^n \frac{1}{k} k = A_n b_n – \sum_{k=1}^{n-1} A_k \cdot 1 \]

つまり

\[ \sum_{k=1}^n k \cdot \frac{1}{k} = n \sum_{k=1}^n \frac{1}{k} – \sum_{k=1}^{n-1}\sum_{i=1}^k \frac{1}{i} \]

となります。