微分積分学
-
ソフトマックス(softmax)関数について解説!具体的に計算する!

ソフトマックス関数の概要 ソフトマックス関数(Softmax function)は、機械学習において、特に分類問題で広く使用される関数です。この関数は、入力ベクトルを受け取り、各要素を0から1の範囲の …
-
テイラーの定理とテイラー展開

テイラーの定理 ここで、\( R_n(x) \) は剰余項(誤差項)で、\( n \) 次のテイラー多項式による近似と実際の関数値との差を表します。 剰余項の形式 剰余項 \( R_n(x) \) に …
-
シグモイド関数と微分・グラフについて
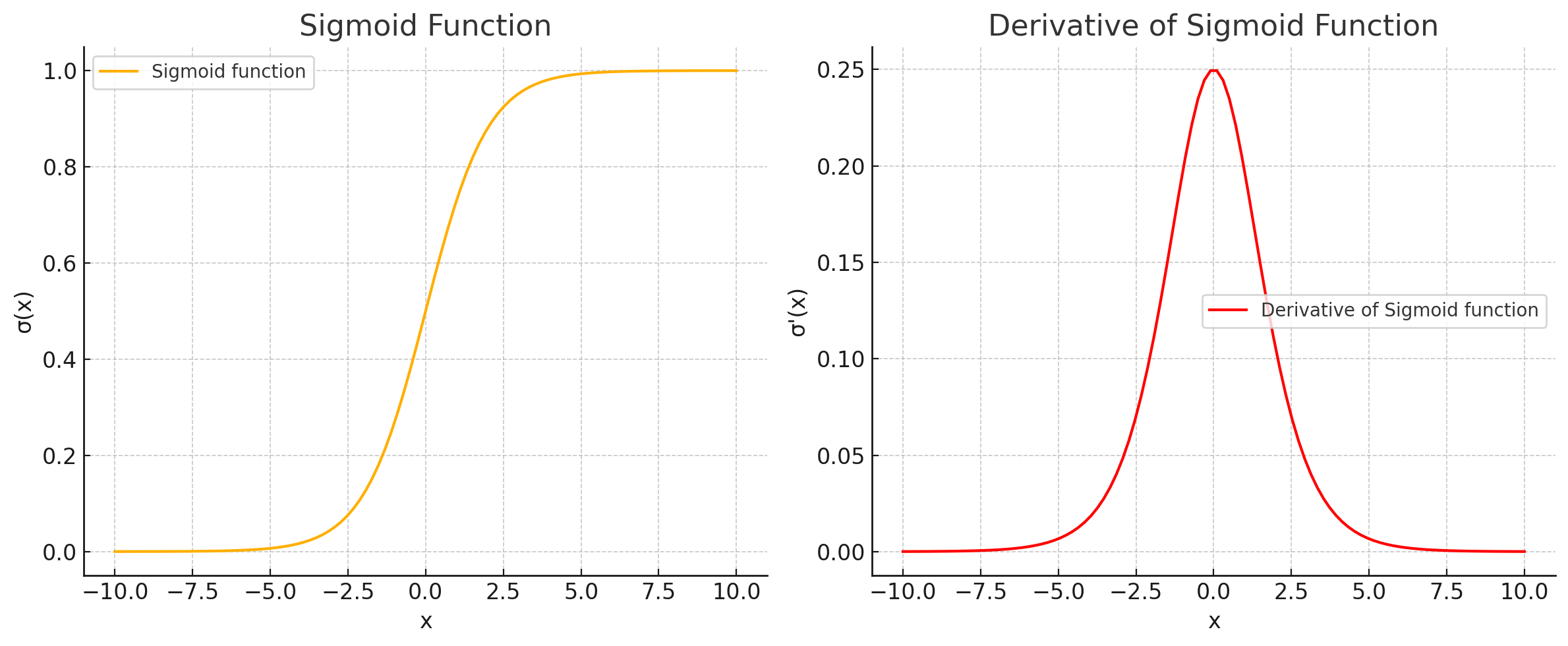
シグモイド関数 シグモイド関数の微分 シグモイド関数 \(\sigma(x)\) の微分を商の微分の規則を使って計算します。まず、商の微分に従って微分します。商の微分の公式は以下の通りです。 \[ \ …
-
双曲線関数の逆関数

双曲線関数とは 双曲線関数の逆関数 1. $\sinh^{-1} x = \log(x + \sqrt{x^2 + 1})$ の証明 関数 $y = \sinh x = \frac{e^ …
-
楕円の面積・周長・楕円率・離心率・焦点の計算ツール
長軸半径と短軸半径を入力することで楕円の面積・長さ・楕円率・離心率・焦点を計算することができます。 楕円の計算 長軸半径a: 短軸半径b: 計算 計算結果 計算式 面積を$S$としたとき、$a$を長軸 …
-
1/6公式・放物線と直線に囲まれる面積の関係について

$\dfrac{1}{6}$公式とは 1/6公式とは、特定の形の定積分において成り立つ計算結果を表した公式です。具体的には、$\alpha$と$\beta$という2つの値の間で、$(x-\alpha) …
-
積の微分と商の微分の証明と例題について

積の微分 積の微分の証明 導関数の定義より、 $$(f(x)g(x))’=\displaystyle\lim_{h \to 0}\frac {f(x+h)g(x+h)-f(x)g(x)}{h}$$ $ …
-
【計算問題付き】対数微分法の計算手順について

対数微分法とは 対数微分法は対数をとることで微分を楽にする方法。微分が困難であるときや計算が複雑な時に用いると計算が楽になることがある。 対数微分法が成り立つ理由 実際に微分の計算をすると、 $$y’ …