微分積分学
-
ガンマ関数の4つの基本的な性質!階乗と特殊関数との関係

ガンマ関数とは? ガンマ関数の性質 ガンマ関数の性質の証明 \(\Gamma(p+1) = p \cdot \Gamma(p)\) 部分積分を使用します。 \[ \Gamma(p+1) = \int_ …
-
数値微分の基本!前進差分法、後退差分法、および中心差分法について
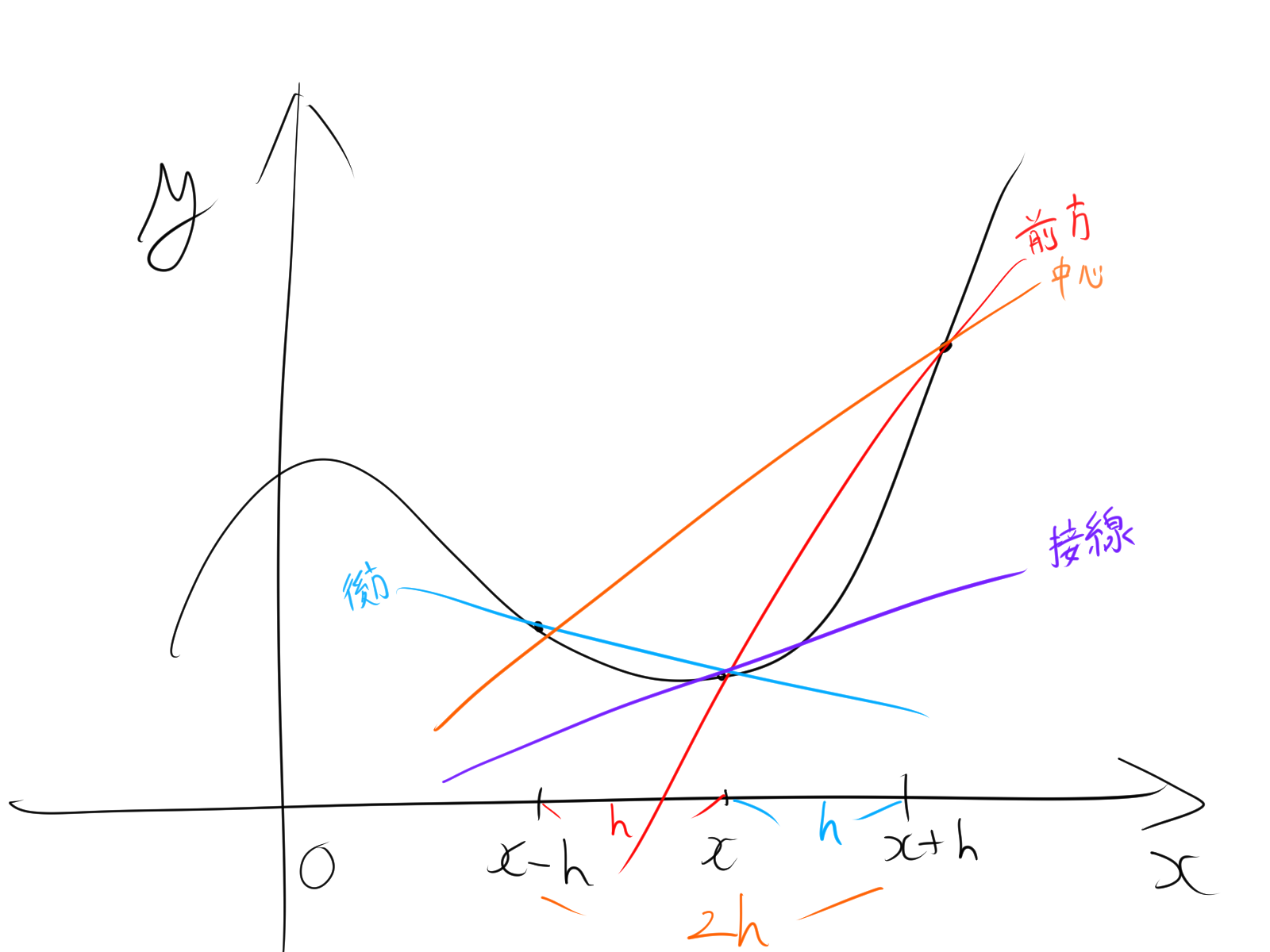
数値微分の基本的な方法 数値微分は、関数の導関数(微分)を数値的に求める手法です。これは、関数が解析的に微分できない場合や、関数の式が知られていない場合に特に有用です。数値微分の基本的な考え方は、関数 …
-
勾配(gradient)について!意味とディープラーニングへの応用について
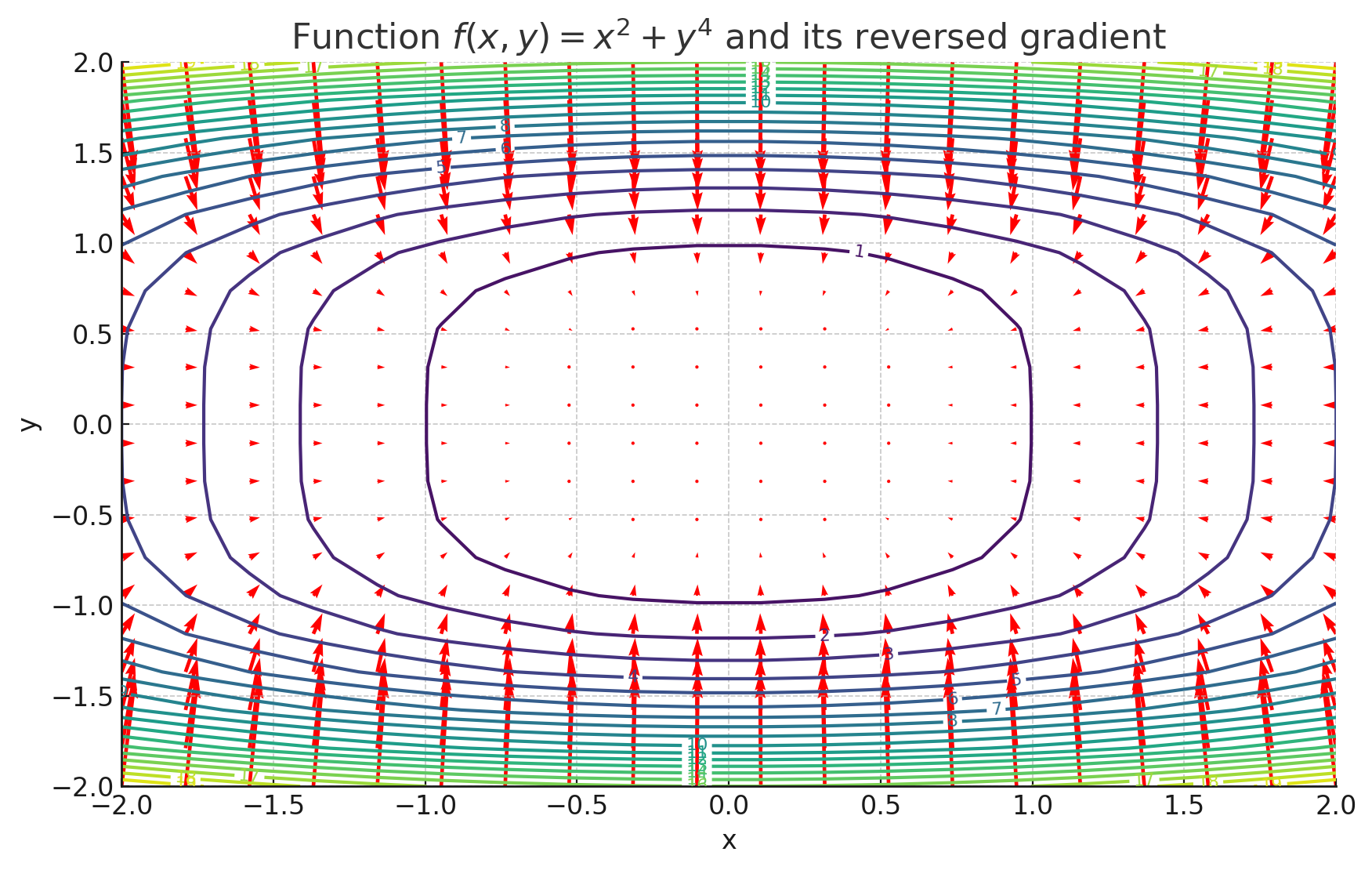
勾配とは 勾配の特徴 勾配の計算の具体例 2変数関数 \( f(x,y) = x^2 + y \) の勾配は、関数の各変数に関する偏微分を計算することで求められます。勾配ベクトルは次のように定義されま …
-
勾配法について!関数の最小値をpythonで求める
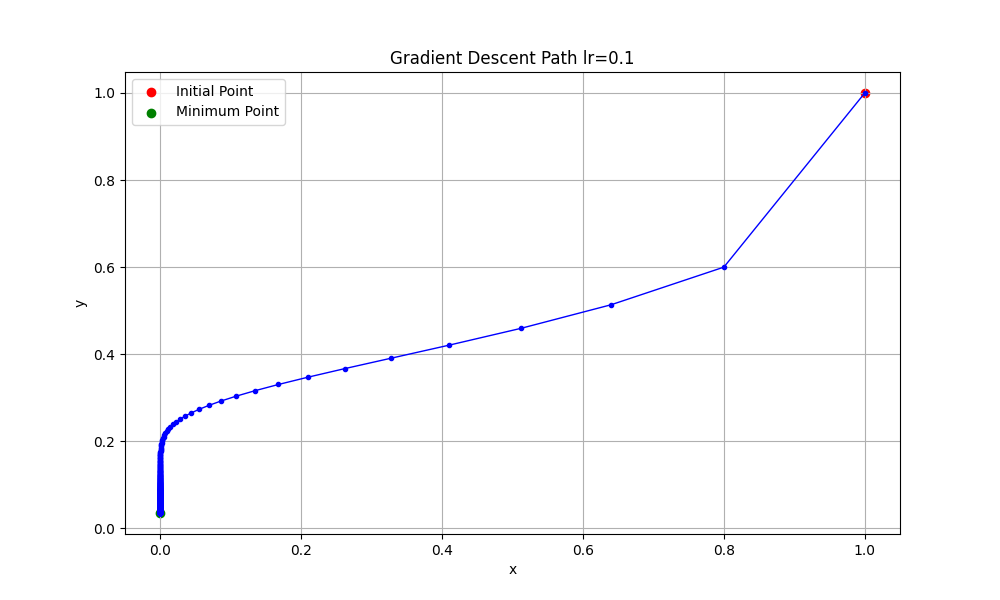
勾配法の手順 勾配法を用いて、関数の最小値を見つけるための手順を示します。 勾配法を用いて最小値を求める 勾配の計算 関数 \( f(x, y) = x^2 + y^4 \) の最小値を勾配法で求める …
-
テイラーの定理とテイラー展開

テイラーの定理 ここで、\( R_n(x) \) は剰余項(誤差項)で、\( n \) 次のテイラー多項式による近似と実際の関数値との差を表します。 剰余項の形式 剰余項 \( R_n(x) \) に …
-
シグモイド関数と微分・グラフについて
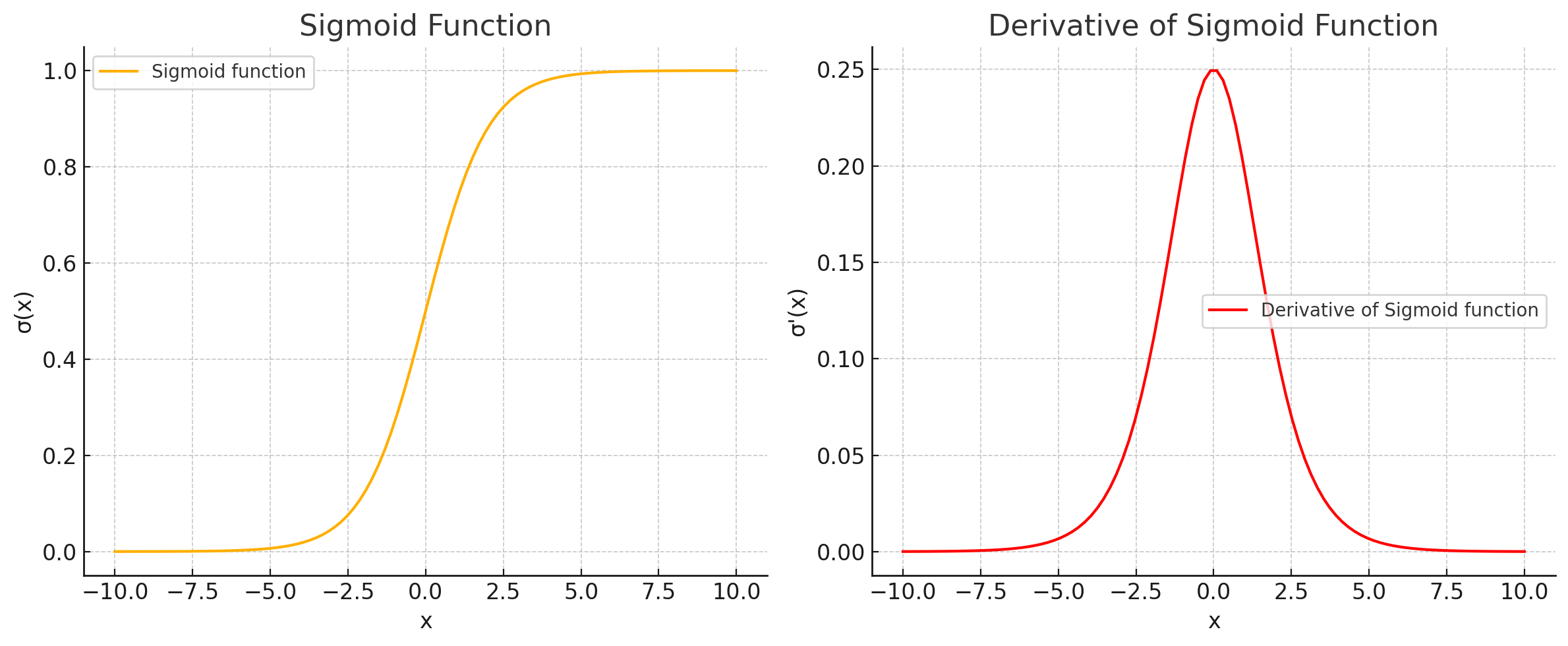
シグモイド関数 シグモイド関数の微分 シグモイド関数 \(\sigma(x)\) の微分を商の微分の規則を使って計算します。まず、商の微分に従って微分します。商の微分の公式は以下の通りです。 \[ \ …
-
双曲線関数の逆関数

双曲線関数とは 双曲線関数の逆関数 1. $\sinh^{-1} x = \log(x + \sqrt{x^2 + 1})$ の証明 関数 $y = \sinh x = \frac{e^ …
-
双曲線関数の逆関数の微分

双曲線関数とは 双曲線関数の逆関数の微分 1. \(\sinh^{-1} x\) の微分 \(y=\sinh^{-1} x\) のとき \(x = \sinh y\) となるため、$\dfrac{dx …