微分積分学
-
オイラーの公式の定義・性質・証明・例題について

オイラーの公式とは オイラーの公式の証明 マクローリン展開による証明 $\sin x,\cos x,e^{ix}$をそれぞれマクローリン展開する。 $\sin x$をマクローリン展開する。 $$\si …
-
微分係数の定義・例題について

微分係数 この式は、平均変化率(ある区間での関数の変化の割合)を \( \Delta x \) が限りなく小さくなるときに考えることで、微分係数を得ます。微分係数が存在する場合、関数 \( f(x) …
-
平均変化率の定義・例題について

平均変化率とは これは、関数 \( f(x) \) のグラフ上の \( (x_1, f(x_1)) \) と \( (x_2, f(x_2)) \) という2つの点を結んだ直線の傾きに対応します。直線 …
-
e^xsinxとe^xcosxの極限・微分・積分・グラフについて
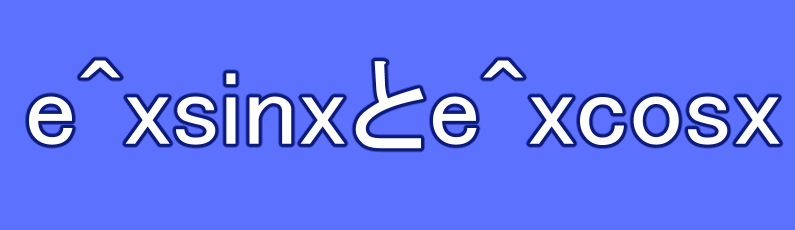
極限 \( x \to \infty \) のときの極限 \( e^x\sin x \) や \( e^x\cos x \) はともに \( e^x \) が指数関数であり、無限大に発散するため、 \ …
-
調和級数の定義・性質・オイラー定数について

調和級数とは 調和級数の性質 オイラー・マスケローニ定数 オイラー・マスケローニ定数$\gamma $は次のように定義されます。 \[ \gamma = \lim_{n \to \infty} \le …
-
argmax、argminの定義・具体例・例題について

argmaxとargminについて argmax・・・argument of the maximum(最大点集合)の略。最大化する引数について。 argmin・・・argument of the mi …
-
楕円積分の意味、ルジャンドルの標準形とヤコビの標準形について

楕円積分とは 楕円積分は、その形状が楕円の長さや面積の計算に関連しています。また、楕円積分は通常、第一種、第二種、および第三種に分類されます。一般的には以下のように定義されます。 楕円積分の登場 第一 …
-
xlogxの極限・微分・積分・グラフについて

極限 方法1($x=\frac{1}{t}$と置く) $x=\frac{1}{t}$と置くと、\( t \to +\infty\) \[ \lim_{x \to +0} x \log x \] $$= …