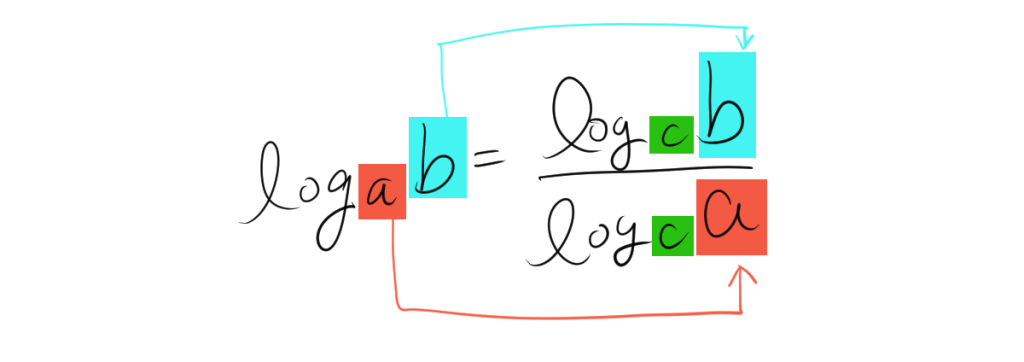【図解】対数の底の変換公式の使い方、証明、例題について

1. 対数の底の変換
対数を扱うとき、特に異なる底の対数を計算するときに便利な公式として「対数の底の変換」があります。この公式を使うことで、異なる底の対数を計算しやすくなります。
1.1. 対数の底の変換公式
\[ \log_a b = \frac{\log_c b}{\log_c a} \]
この公式を使うことで、底を自由に変換することができます。例えば、底\(a\)の対数を自然対数(底\(e\))や常用対数(底\(10\))に変換することが可能です。
1.2. 対応関係
2. 公式の証明
まず、対数の定義より、
\[ \log_a b = x \quad \Leftrightarrow \quad a^x = b \]
この式を底\(c\)で対数を取ると、
\[ \log_c (a^x) = \log_c b \]
対数の法則より、
\[\begin{align*} x \cdot \log_c a &= \log_c b \\ \log_c a &=\frac{\log_c b}{x} \end{align*}\]
ここで、\(x = \log_a b\)なので、
\[ \log_a b = \frac{\log_c b}{\log_c a} \]
3. 対数の変換の例題
3.1. 例題 1
底の変換公式を使います。よって、
\[ \log_2 1024 = \frac{\log_4 1024}{\log_4 2} \]
まず、\( \log_4 1024 \) を計算します。
1024 は \( 4 \) の何乗かを考えると、まず \( 1024 = 2^{10} \) であり、次に \( 2^{10} = \left(4^{\frac{1}{2}}\right)^{10} = 4^5 \) となります。したがって、
\[ \log_4 1024 = 5 \]
次に、\( \log_4 2 \) は \( 2 = 4^{\frac{1}{2}} \) より
\[ \log_4 2 = \frac{1}{2} \]
よって、
\[ \log_2 1024 = \frac{5}{\frac{1}{2}} = 10 \]
3.2. 例題 2
底の変換公式を使います。
\[ \log_3 81 = \frac{\log_9 81}{\log_9 3} \]
まず、\( \log_9 81 \) を計算します。
\( 81 = 9^2 \) なので、 \[ \log_9 81 = 2 \]
次に、\( \log_9 3 \) ですが、\( 3 = 9^{\frac{1}{2}} \) なので
\[ \log_9 3 = \frac{1}{2} \]
よって、
\[ \log_3 81 = \frac{2}{\frac{1}{2}} = 4 \]
3.3. 例題 3
まず底の変換公式を使って、\( \log_3 8 \) を変換します。
\[ \log_3 8 = \frac{\log_2 8}{\log_2 3} = \frac{3}{\log_2 3} \]
したがって、
\[ \log_2 3 \cdot \log_3 8 = \log_2 3 \cdot \frac{3}{\log_2 3} =3\]
3.4. 例題 4
底の変換公式を使います。よって、
\[ \log_{\frac{1}{7}} 49 = \frac{\log_7 49}{\log_7 \left(\frac{1}{7}\right)} \]
\( 49 = 7^2 \) 、\( \frac{1}{7} = 7^{-1} \) なので、
よって、
\[ \log_{\frac{1}{7}} 49 =\frac{\log_7 49}{\log_7 \left(\frac{1}{7}\right)} = \frac{2}{-1} = -2 \]