行列の積の計算方法・性質・具体例・添え字の対応関係・例題について
1. 行列の積
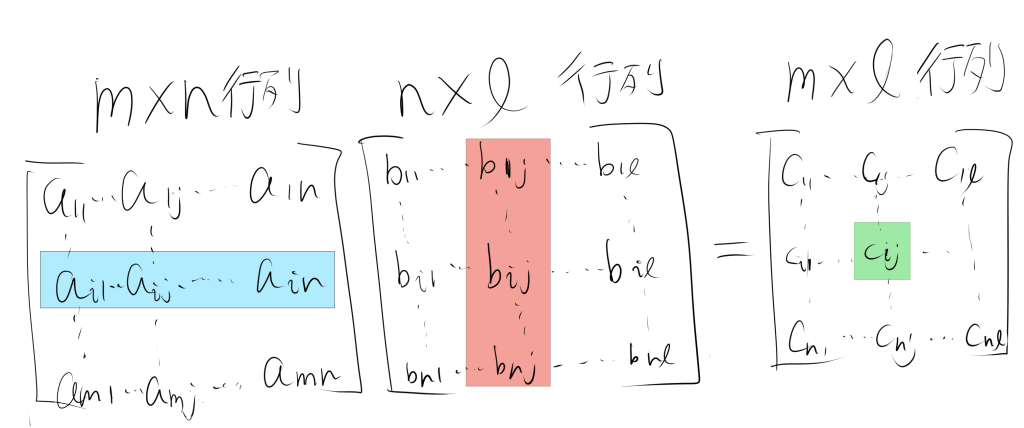
行列の積は以上の画像のように行列の$c_{ij}$の成分（緑色の部分）が、青色の部分と赤色の部分の積の和となるような計算のことです。
行列の積ABは以下のようにあらわすことができます。
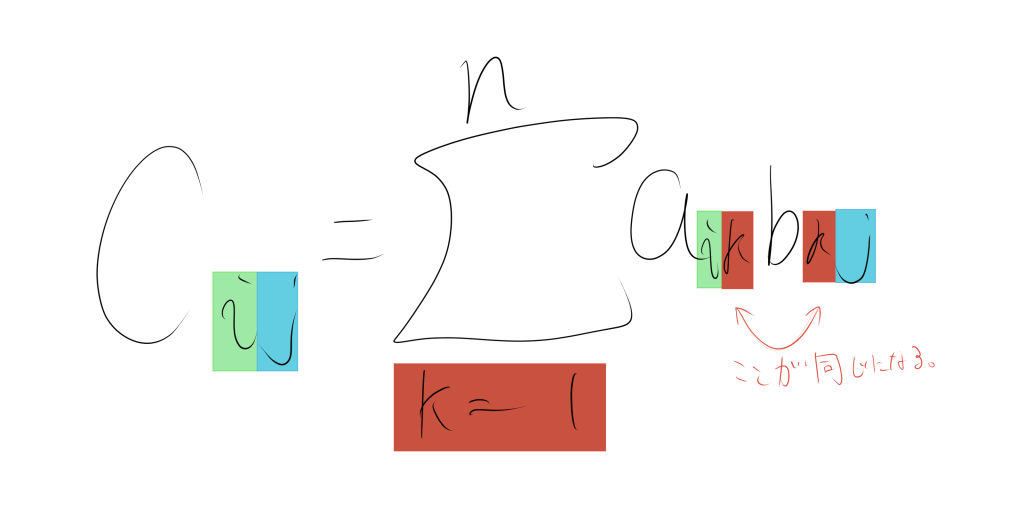
$$\Large c_{ij}=\displaystyle\sum_{k=1}^n a_{ik}b_{kj}$$
1.1. 添え字の対応
添え字の対応を色を用いて表すと以下のようになります。
1.2. 行列のサイズ
行列の積の結果で得られる行列のサイズは、$m×n$行列と$n×l$行列の積であった場青、$m×l$行列になります。また、行列の積ABにおいて、Aの列数とBの行数が一致していないと、計算ができません。
2. 行列の積の例
行列の積の具体例を行いたいと思います。$2×2$行列を例にしてみましょう。$A= \begin{pmatrix} 2 & 3 \\ 4 & 1 \\ \end{pmatrix}$ $B=\begin{pmatrix} 5 & 7 \\ 6 & 8 \\ \end{pmatrix}$としたときの行列の積$AB$を求める。
$AB = \begin{pmatrix} 2 & 3 \\ 4 & 1 \\ \end{pmatrix} \begin{pmatrix} 5 & 7 \\ 6 & 8 \\ \end{pmatrix} $
$= \begin{pmatrix} 2\times5+3\times6 & 2\times7+3\times8 \\ 4\times5+1\times6 & 4\times7+1\times8 \\ \end{pmatrix} $
$= \begin{pmatrix} 28 & 38 \\ 26 & 36 \\ \end{pmatrix} $
2.1. 行列の積の順序を逆にすると
先ほどは行列の積$AB$を求めてみましたが、今度は行列の積$BA$を求めてみましょう。
$AB =\begin{pmatrix} 5 & 7 \\ 6 & 8 \\ \end{pmatrix} \begin{pmatrix} 2 & 3 \\ 4 & 1 \\ \end{pmatrix} $
$ = \begin{pmatrix} 5\times2+7\times4 & 5\times3+7\times1 \\ 6\times2+8\times4 & 6\times3+8\times1 \\ \end{pmatrix}$
$ = \begin{pmatrix} 38 & 22 \\ 44 & 26 \\ \end{pmatrix} $
このように、行列の積$AB$とはまた違う行列の計算結果が得られました。このように、行列の積の順序は入れ替えると、整数の掛け算と違って、必ず計算結果は同じにはなりません。つまり、$AB \neq BA$ となるのです。
3. 例題
次の行列 \( A \) と \( B \) の積 \( C=AB \) を計算しなさい。
行列 \( A \) は \( 2 \times 3 \) 行列、行列 \( B \) は \( 3 \times 2 \) 行列とします。
\[ A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix} \quad B = \begin{pmatrix} 7 & 8 \\ 9 & 10 \\ 11 & 12 \end{pmatrix} \]
行列 \( C \) の形は \( 2 \times 2 \) 行列になります。
行列 \( C \) の第1行第1列の要素:
\[ C_{11} = 1 \times 7 + 2 \times 9 + 3 \times 11 = 7 + 18 + 33 = 58 \]
行列 \( C \) の第1行第2列の要素:
\[ C_{12} = 1 \times 8 + 2 \times 10 + 3 \times 12 = 8 + 20 + 36 = 64 \]
行列 \( C \) の第2行第1列の要素:
\[ C_{21} = 4 \times 7 + 5 \times 9 + 6 \times 11 = 28 + 45 + 66 = 139 \]
行列 \( C \) の第2行第2列の要素:
\[ C_{22} = 4 \times 8 + 5 \times 10 + 6 \times 12 = 32 + 50 + 72 = 154 \]
したがって、行列の積 \( C \) は次のようになります。
\[ C = \begin{pmatrix} 58 & 64 \\ 139 & 154 \end{pmatrix} \]
