確率・統計
-
連続型確率変数の期待値と分散・定義・例題について

期待値 期待値は、確率変数の平均値、つまり「期待される値」を表します。 連続型確率変数の期待値 ここでも、各値 \( x \) に対して、その確率密度 \( f(x) \) を掛けたものを全て積分して …
-
不偏推定量の定義・具体例について

不偏推定量とは 不偏推定量とは、母数の推定に使用される推定量の中で、その期待値が推定しようとする母数と一致するものを指します。つまり、不偏推定量は、サンプルから得られた推定値の平均(期待値)が真の母数 …
-
離散型確率変数の期待値と分散・定義・練習問題について

期待値 期待値は、確率変数の平均値、つまり「期待される値」を表します。 離散型確率変数の期待値 これは、各値 \( x_i \) にその確率 \( p_i \) を掛けたものを全て足し合わせたものです …
-
標本平均の期待値・分散・不偏推定量・性質・練習問題について

標本平均とは 標本平均とは、ある集団(母集団)から抽出したデータの平均値を指します。標本平均は、母集団全体の平均(母平均)を推定するために用いられる重要な指標です。 標本平均の計算方法 例えば、5つの …
-
例題で解説する指数分布とポアソン分布の違い
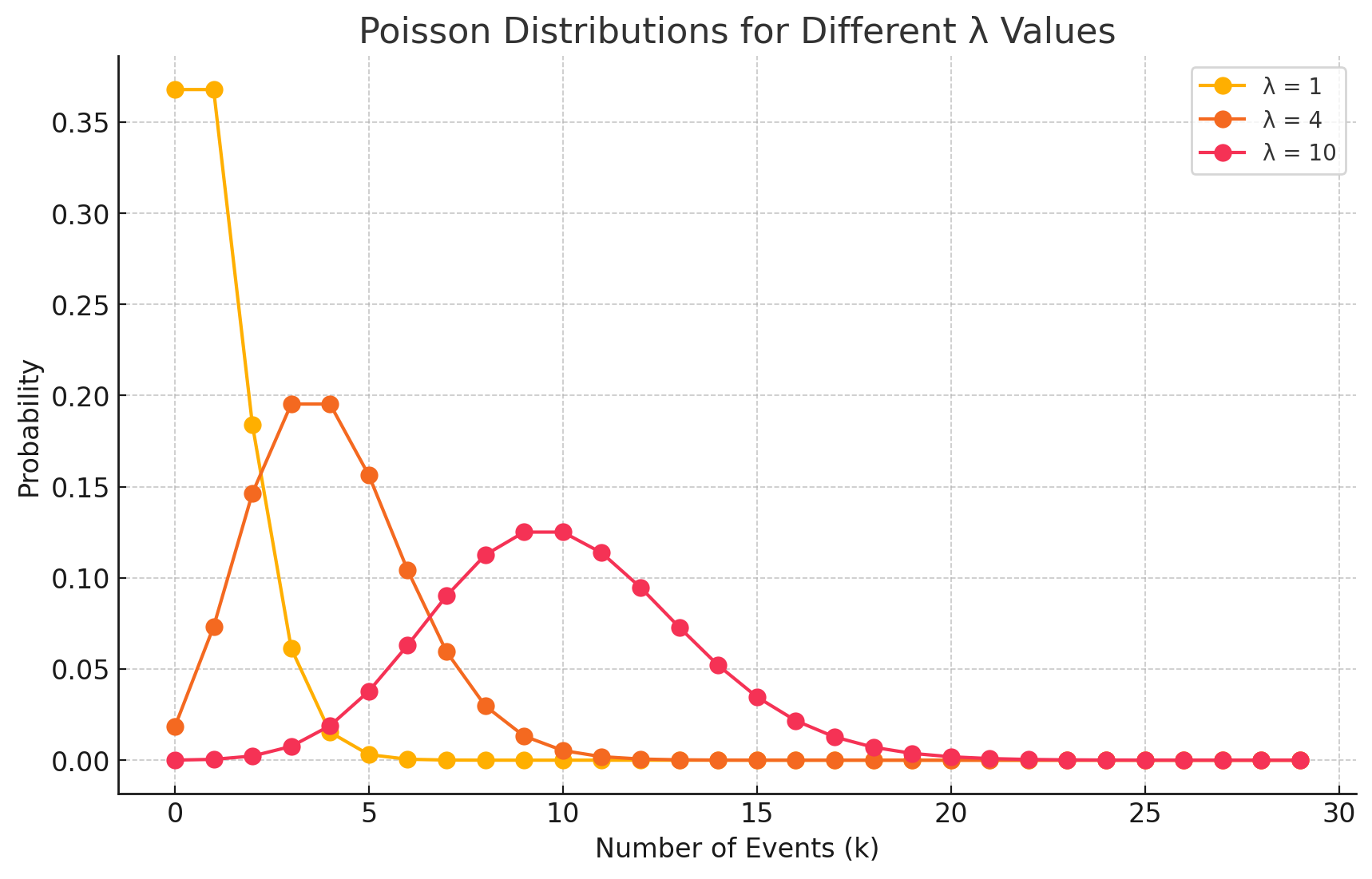
指数分布とポアソン分布の違い ポアソン分布 (Poisson Distribution) 確率変数: ポアソン分布の確率変数は、一定の時間または空間内で発生するイベントの回数を表します。この確率変数は …
-
ベータ関数の基本的な性質!複数の積分表示や関係式について
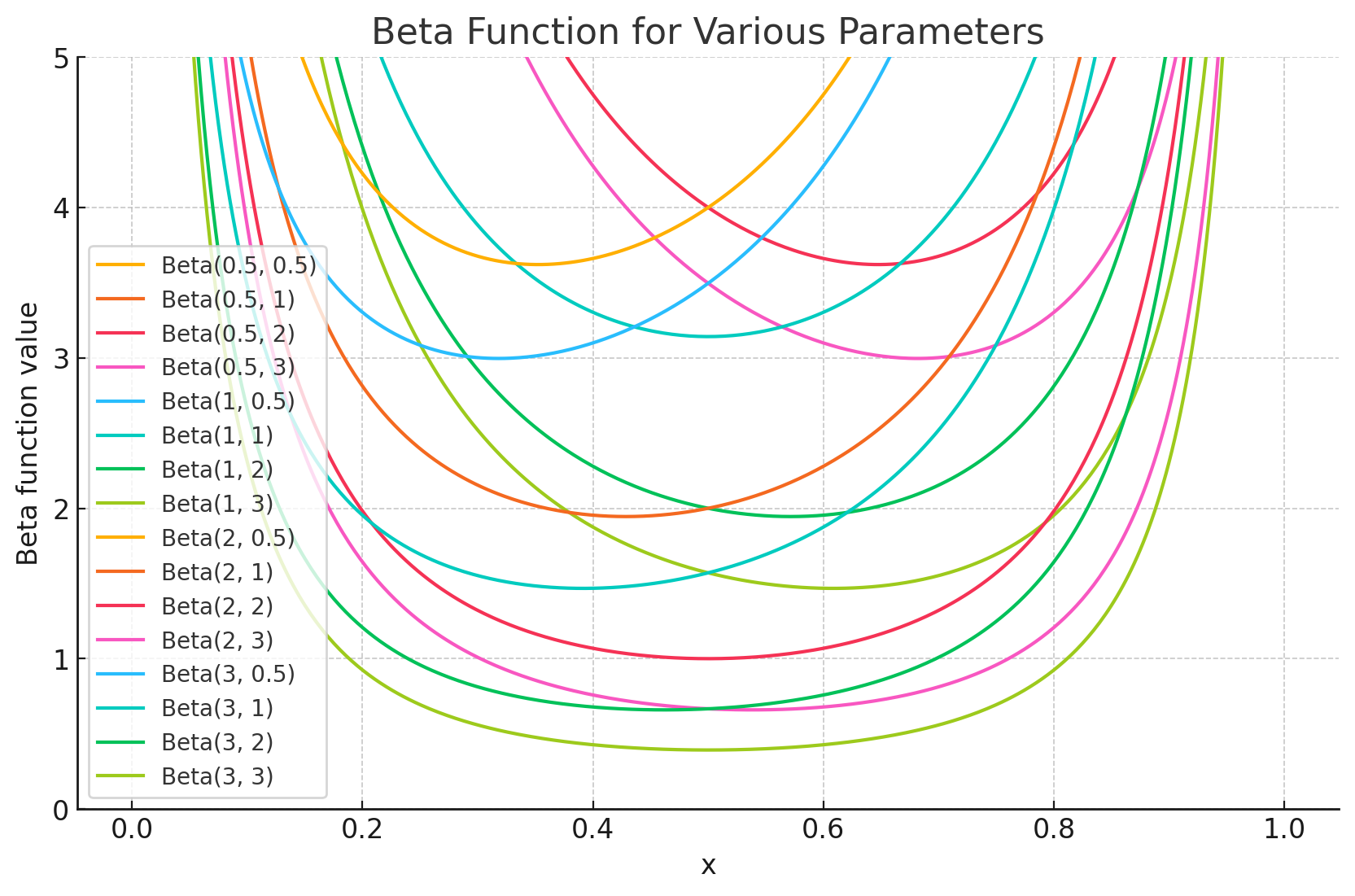
ベータ関数とは https://www.math-joy-life.com/gamma-function-nature/ ガンマ関数の表示 ガンマ関数の定義より、ガンマ関数の積を計算します。 \[ \ …
-
カイ(χ)2乗分布について!ガンマ関数と確率密度関数の関連性

χ²分布とは このXは自由度kのχ²分布に従います。 基本的な性質 自由度 (degrees of freedom, df): χ²分布は自由度(df)というパラメータによって特徴づけられます。自由度 …
-
ガンマ関数の4つの基本的な性質!階乗と特殊関数との関係

ガンマ関数とは? ガンマ関数の性質 ガンマ関数の性質の証明 \(\Gamma(p+1) = p \cdot \Gamma(p)\) 部分積分を使用します。 \[ \Gamma(p+1) = \int_ …