分野別
✔ 確率・統計




✔ IT用語
✔ 機械学習・ディープラーニング




✔ 微分積分学
新着記事
-
勾配(gradient)について!意味とディープラーニングへの応用について
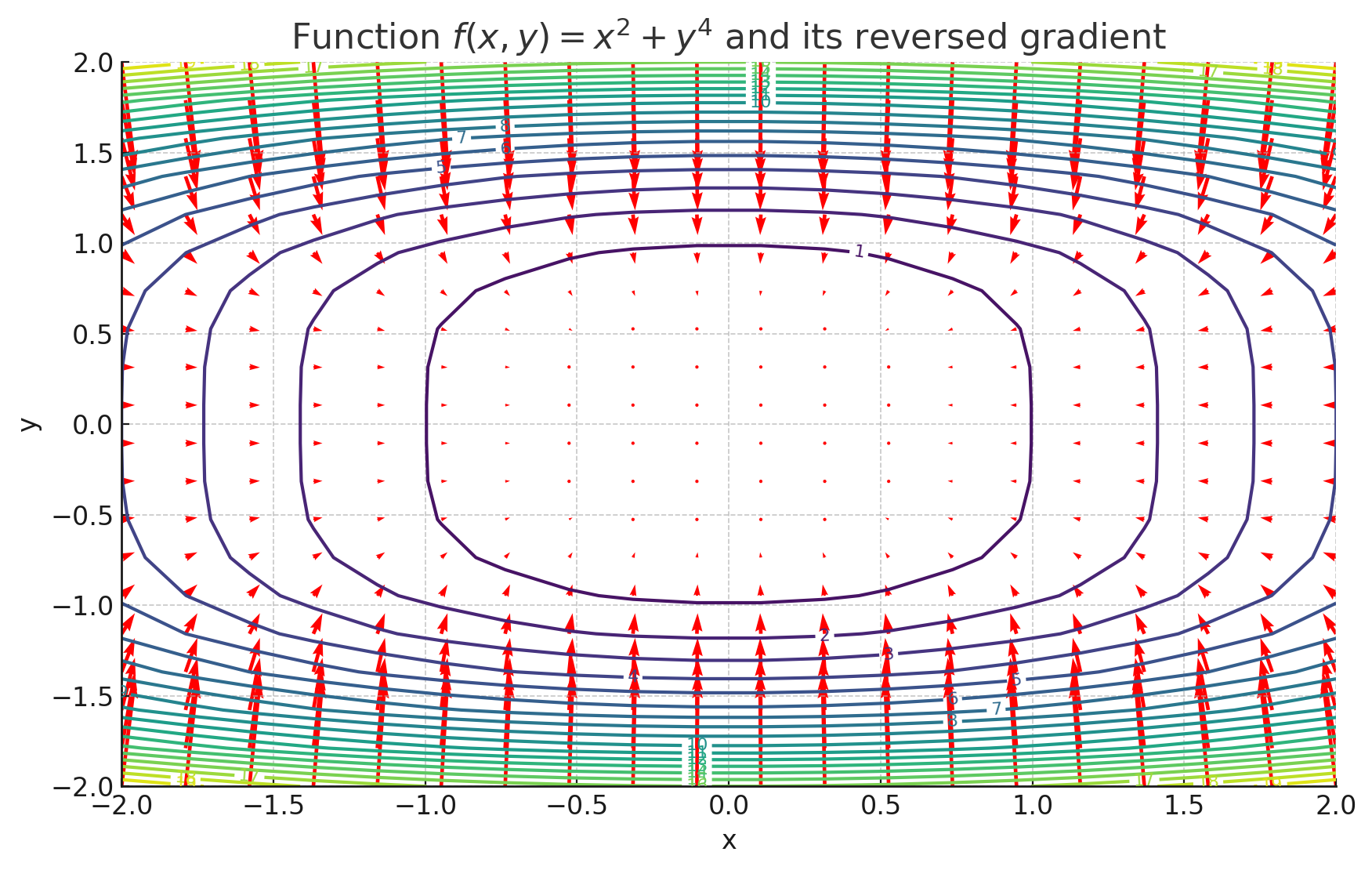
勾配とは 勾配の特徴 勾配の計算の具体例 2変数関数 \( f(x,y) = x^2 + y \) の勾配は、関数の各変数に関する偏微分を計算することで求められます。勾配ベクトルは次のように定義されま …
-
deepsetのbert-large-uncased-whole-word-masking-squad2の使い方!Question Answering

BERTとは BERT(Bidirectional Encoder Representations from Transformers)はencoderのみの言語モデルです。bert-large-un …
-
bert-large-uncased を使ってみよう!MLMを試す!

BERTとは BERT(Bidirectional Encoder Representations from Transformers)はencoderのみの言語モデルです。bert-large-un …
-
bert-base-casedの使い方!Case Sensitiveを確認する!

BERTとは BERT(Bidirectional Encoder Representations from Transformers)はencoderのみのモデルです。bert-base-cased …
-
bert-base-uncasedの使い方!マスクされた単語を推測する!

BERTとは BERT(Bidirectional Encoder Representations from Transformers)はencoderのみのモデルです。bert-base-uncas …
-
連続型と離散型のチェビシェフの不等式の証明について

チェビシェフの不等式 チェビシェフの不等式は連続型、離散型の両方で成り立ちます。 連続型の場合のチェビシェフの不等式の証明 分散 \(\sigma^2\) は次のように定義されます。 \[ \sigm …
-
PythonでのWebスクレイピング:SeleniumとBeautiful Soupの連携
Webスクレイピングとは? Webスクレイピングの基本概念 Webスクレイピングとは、インターネット上のウェブサイトからデータを抽出する技術のことを指します。近年、Webスクレイピングはデータ収集の手 …
-
mixhostのサーバースペックについて解説!リソースについても
mixshotのサーバースペック 構成 LiteSpeed対応 mixhostはLiteSpeedに対応しているので、LsCacheを使用することで高速化することができます。LaravelのLsCa …
-
圧倒的満足度!mixhostのレンタルサーバーについて解説!
圧倒的満足度!mixhostのレンタルサーバー レンタルサーバーのmixhost(ミックスホスト)は、多くの利用者から高い評価を受けています。 2021年8月期 日本マーケティングリサーチ機構調べ 9 …
-
周波数と波長の関係式(v=fλ)を理解する!単位についても確認!

基本的な関係式 用語の説明 波の速度(\( v \)): 波が媒体を通って進む速さを表します。 単位は通常メートル毎秒(m/s)です。 振動数(\( f \)): 波が1秒間に何回振動するかを示します …
-
ソフトマックス(softmax)関数について解説!具体的に計算する!

ソフトマックス関数の概要 ソフトマックス関数(Softmax function)は、機械学習において、特に分類問題で広く使用される関数です。この関数は、入力ベクトルを受け取り、各要素を0から1の範囲の …
-
pythonのmap関数でTypeError: 'xxx' object is not iterable:問題と解決策

問題のコード def my_function(a): return a * 2 map(my_function, 5) —————————————- …
-
pythonのmapでAttributeError: 'map' object has no attribute 'xxxx'

問題のコード def my_function(a): return a**2 m = map(my_function, [1, 2, 3]) m.append(4) print(m) – …
-
pythonのmapでTypeError: xxxx() missing 1 required positional argument: 'b':問題と解決策

問題のコード def my_function(a, b): return a + b result=list(map(my_function, [(1, 2), (3, 4, 5)]) ) print …
-
pythonのmap関数の使い方について解説!リストの要素に関数を適用。

map関数とは map関数は、Pythonで非常に便利な高階関数の一つです。map関数を使うことで、ある関数をイテレータ(リストやタプルなど)の各要素に適用することができます。以下に、map関数の使い …
-
Laravelでパスワードを間違える!SQLSTATE[HY000] [1045] Access denied for user 'root'@'localhost' (using password: YES):原因と解決策
SQLSTATE[HY000] [1045] Access denied for user ‘root’@’localhost’ (using password: YES) エラーの概要 SQLSTA …







