分野別
✔ 確率・統計




✔ IT用語
✔ 機械学習・ディープラーニング




✔ 微分積分学
新着記事
-
論理和標準形と論理積標準形の定義・性質・例題について

論理和標準形とは 論理和標準形は、論理式を「論理積の論理和」の形で表したものです。具体的には、いくつかの「リテラル(変数やその否定)」の論理積をとり、それらの論理積の論理和をとった形式です。 \[ ( …
-
ダランベールの判定法の定義・例題・性質について

ダランベールの判定法とは ダランベールの判定法は無限級数の収束性を調べるための手法です。特に、この判定法は正項級数に適用されます。ここでの「正項級数」とは、級数の全ての項が非負の数であるという意味です …
-
文脈自由文法と導出木、 最左導出と最右導出の性質と例について

文脈自由文法とは 文脈自由文法 (Context-Free Grammar, CFG) は、形式言語理論で使われる文法の一種です。 基本的な要素 ここで、この数式の意味は次のようになっています。 \( …
-
モンテカルロ法を使って円周率を計算してみよう

モンテカルロ法 モンテカルロ法を用いて円周率(π)を求める方法は、乱数を用いて円の面積と正方形の面積の比率からπを近似的に求めるものです。 ステップ モンテカルロ法では、次のようなステップを踏みます。 …
-
和暦西暦相互変換ツール いまって西暦何年?
このツールは、西暦と和暦(日本の元号を用いた年号)の相互変換を簡単に行うことができます。 西暦から和暦への変換ツール 西暦を入力: 変換 使い方 西暦を入力 「西暦を入力」のラベルの下にある入力フィー …
-
二次形式と標準形、最大値最小値について

二次形式の定義 線形代数において、二次形式は特定の形を持つ関数で、主にベクトルと行列を使って表されます。二次形式の一般的な定義は次のようになります。 ここで、$\mathbf{x} = \begin{ …
-
正則行列・逆行列の性質と具体例について

正則行列とは ここで、\( I \) は単位行列(全ての対角成分が1で、その他の成分が0の行列)です。逆行列 は通常、\( A^{-1} \) と表記されます。 正則行列の性質 行列 \( A \) …
-
固有値の積と行列式・計算問題・固有値計算の検算テクニックについて

固有値の積と行列式 行列の固有値と行列式 行列 \( A \) の固有値とは、次の固有値方程式を満たすスカラー \( \lambda \) のことです。 \[ A \mathbf{v} = \lamb …
-
上三角行列の具体例と性質について解説

上三角行列の定義 上三角行列(じょうさんかくぎょうれつ、Upper Triangular Matrix)は、正方行列の一種で、行列の下半分の成分がすべてゼロであるものを指します。 ここで、\( a_{ …
-
冪零行列の具体例と性質について解説

冪零行列とは 冪零行列(べきれいぎょうれつ、nilpotent matrix)とは、ある整数 \( k \) に対して、その行列を \( k \) 回自乗(自分自身を掛ける)すると零行列(全ての要素が …
-
SymPyでベクトルの外積を計算する方法について

外積とは 外積は次の記事で解説しています。 https://www.math-joy-life.com/crossdot/ SymPyを利用した外積の計算 SymPyを使用してベクトルの外積を計算する …
-
pandasで簡単にCSVファイルを出力・編集のする方法について

CSVファイルに書き込む pandasのデータをCSVファイルに出力するためには、pandasのto_csvメソッドを使用します。次はその基本的な使い方の例です。 import pandas as p …
-
matplotlibで日本語の文字化けを解消する!UserWarning: Glyph xxxx (\N{KATAKANA LETTER KA}) missing from font(s) xxxx.
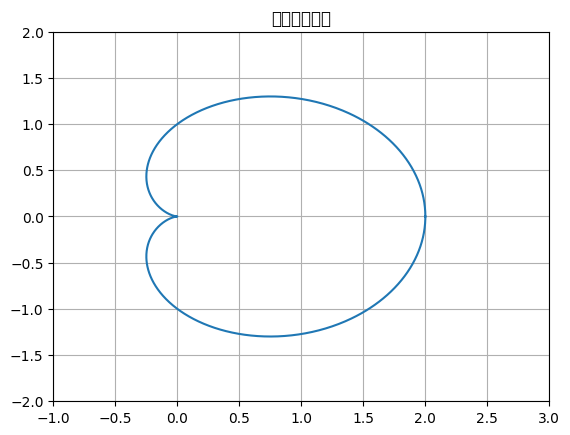
グラフのプロット matplotlibを使用してカージオイドのグラフをプロットします。 import matplotlib.pyplot as plt import numpy as np def c …
-
1/2mv^2とは何か?運動エネルギーの基礎

運動エネルギーとは 質量(\( m \)):物体の質量は、その物体が持つ物質の量を示します。質量が大きいほど、同じ速度で運動する場合の運動エネルギーも大きくなります。 速度(\( v \)):物体の速 …
-
ポリガンマ関数の漸化式とPythonのSciPyを利用した数値計算

ポリガンマ関数とは ディガンマ関数については次の記事で解説しています。 https://www.math-joy-life.com/digamma-function/ ポリガンマ関数の漸化式 $n$ …
-
Python標準ライブラリcollectionsのCounterを使い方!要素の出現回数を手軽に集計

Pythonには、データの出現回数を簡単に集計できるCounterという機能が標準で用意されています。例えば、「このリストの中で一番多い要素は?」といった集計が、たった一行のコードで可能になります。 …







